什么情况下，积分和求导可以交换顺序？_盛煌-盛煌娱乐-盛煌全球注册认证站

欢迎浏览我公司网站！！

行业资讯

什么情况下，积分和求导可以交换顺序？

时间: 2023-08-19浏览次数：

谢邀：这不是一个简单的问题，我们先限定为一维的情况。这个情况下，我们假定的情况下，一个非常trivial的结论是，如果和都是连续的，那么这个问题就是微积分基本定理：,不假定这个条件，这个式子都不会成立，这个问题也就失去了价值。一个函数是可导的，自然是连续的，所以上面的式子失职上问什么样的函数满足下面这个

谢邀： 这不是一个简单的问题，我们先限定为一维的情况。这个情况下，我们假定 $f(a)=0$ 的情况下，一个非常trivial的结论是，如果 $f$ 和 $f'$ 都是连续的，那么这个问题就是微积分基本定理：
$\\frac{d}{dx}\\int_a^x f(t)dt=f(x)=f(x)-f(a)=\\int_a^xf'(t) dt$ ,
不假定 $f(a)=0$ 这个条件，这个式子都不会成立，这个问题也就失去了价值。

一个函数是可导的，自然是连续的，所以上面的式子失职上问什么样的函数满足下面这个等式：
$f(b)-f(a)=\\int_a^b f'(t)dt$ 。
我们接下来都不再要求 $f(a)=0$ ，因为只要某个函数 $f$ 满足上面这个式子，我们可以构造
$f_1(t)=f(t)-f(a)$ ,这个自然满足全部条件。

天真的少年（少女）是不是幻想只要 $f$ 可导，式子
$f(b)-f(a)=\\int_a^b f'(t)dt$ 。

就无条件成立了？
幻想可以被下面几个蛋疼的例子打破：

例子1:这个例子极端复杂，目的在于说明一个问题：即使一个函数可导，也不代表这个导数可积。
我这里给一个比较简单的例子吧，设
对于 $x\ eq 0$ , $F(x)=x^2\\sin\\frac{1}{x^2}$ , $F(0)=0$ ，它的导数是
$f(x)=2x\\sin \\frac{1}{x^2}-\\frac{2}{x}\\cos\\frac{1}{x^2}, \\, x\ eq 0, f(0)=0$ ,
但是 $f(x)$ 在0点附近不是黎曼可积的，这一点不难证明，因为达布上和和达布下和不一致。
数学家还构造了一个函数 $H$ ,使得 $H'$ 处处存在，但是无处单调，而且 $H'$ 本身是不可积分的。换句话说，你不能指望
$f(b)-f(a)=\\int_a^b f'(t)dt$
无条件成立！（具体构造请看《实分析中的反例》）

例子2: 我继续打破另外一个幻觉：即使一个函数可积，也不代表这个函数积分出来的函数的导数和自己相等。我们构造一个函数 $g$ 使得 $\\frac{d}{dx}\\int_0^x g(t)dt$ 和 $g(x)$ 在每个区间上都有一个不同的点。
设对于 $x=\\frac{p}{q}$ (为一个有理数，而且可以表示为不可约素数之比),定义 $g(x)=\\frac{1}{p}$ ，其他的点定义为0. 这这个函数是黎曼可积的，而且 $\\int_0^x g(t)dt=0$ ，所以自然有 $\\frac{d}{dx}\\int_0^x g(t)dt$ 和 $g(x)$ 几乎处处不同

一个比较好的结果是这样的（来自rudin）：

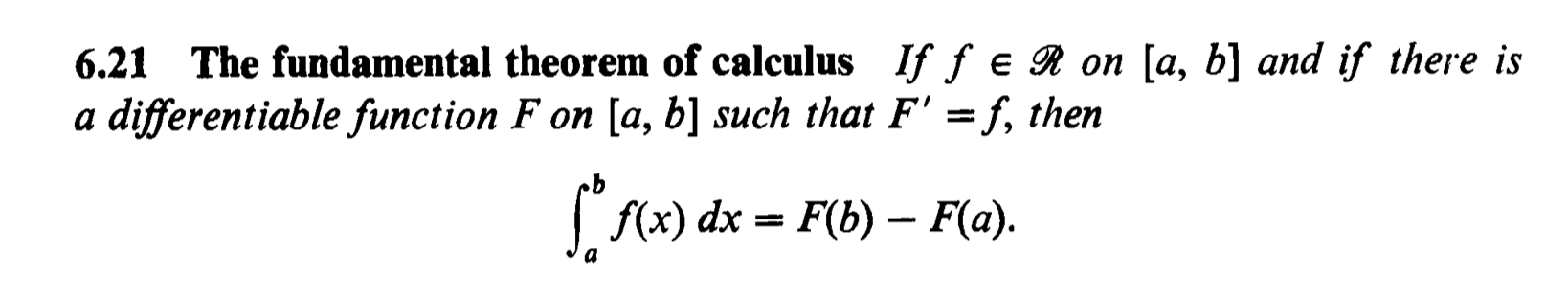
其中 $f\\in \\mathfrak{R}$ (就是那个花写的)意思是黎曼可积分。也就是说一个 $f$ 可微分，而且它的导数是黎曼可积的，那么

$f(b)-f(a)=\\int_a^b f'(t)dt$

成立。

如果把黎曼积分改成勒贝格积分，问题会变得复杂一点，懂勒贝格积分的人也许会猜测：

一个 $f$ 几乎处处微分，而且它的导数是勒贝格可积的，那么

$f(b)-f(a)=(L)\\int_a^b f'(t)dt$

成立。这是错的，例子也来自rudin，里面构造的函数叫cantor函数，具有非常有趣的性质：

对待这个问题，一个靠谱的结论是论：如果 $f$ 是绝对连续的，那么这个函数可以满足

$f(b)-f(a)=\\int_a^b f'(t)dt$ ，（这里的积分是勒贝格积分，而不是黎曼积分）

什么是绝对连续，是这个意思：对于任意的 $\\epsilon>0,\\exists \\delta>0$ ，使得当 $a_1<a_2<\\cdots<a_n$ , $\\sum (a_{n+1}-a_n)\\leq \\delta$ 的时候，必然有 $\\sum|f(a_{n+1})-f(a_n)|\\leq \\epsilon$

参考：实分析中反例

物理问题中基本上都可以。

我的理解与dhchen的不同。我认为题主问的是在什么条件下有

$\\frac{d}{dt}\\int_a^bf(x,t)\\, dx=\\int_a^b\\frac{\\partial }{\\partial t}f(x,t)\\,dx$

费曼写过他上学的时候用这个技术解决了很多积分的计算问题：

One thing I never did learn was contour integration. I had learned to do integrals by various methods shown in a book that my high school physics teacher Mr. Bader had given me. One day he told me to stay after class. "Feynman," he said, "you talk too much and you make too much noise. I know why. You're bored. So I'm going to give you a book. You go up there in the back, in the corner, and study this book, and when you know everything that's in this book, you can talk again." So every physics class, I paid no attention to what was going on with Pascal's Law, or whatever they were doing. I was up in the back with this book: Advanced Calculus, by Woods. Bader knew I had studied Calculus for the Practical Man a little bit, so he gave me the real works—it was for a junior or senior course in college. It had Fourier series, Bessel functions, determinants, elliptic functions—all kinds of wonderful stuff that I didn't know anything about. That book also showed how to differentiate parameters under the integral sign—it's a certain operation. It turns out that's not taught very much in the universities; they don't emphasize it. But I caught on how to use that method, and I used that one damn tool again and again. So because I was self-taught using that book, I had peculiar methods of doing integrals. The result was, when guys at MIT or Princeton had trouble doing a certain integral, it was because they couldn't do it with the standard methods they had learned in school. If it was contour integration, they would have found it; if it was a simple series expansion, they would have found it. Then I come along and try differentiating under the integral sign, and often it worked. So I got a great reputation for doing integrals, only because my box of tools was different from everybody else's, and they had tried all their tools on it before giving the problem to me.

Folland的实分析书里给了一个这个等式成立的较弱的条件。证明的基本想法是把导数写成差分的极限，然后用控制收敛定理交换积分和求极限的顺序：

如果要看数学分析的书，可以读卓里奇的第十七章含参量积分。那里的条件要强一些（偏导数连续）。

我看小平邦彦复分析的时候遇到的积分跟求导的交换情况也是积分跟偏导的交换，这个问题有答主讲了很弱的条件，可见Folland的实分析。下面的是有比较强条件的数学分析里面的答案，偏导连续这个条件会更加常用一点。

或者，这个问题的解答可以在国内或俄罗斯那边数学分析教材的含参变量积分那一章找到答案，一般的教材都会有。就比如某数分教材下有：

假设所问的问题是以下等式成立条件:

$\\frac{\\mathrm{d}}{\\mathrm{d}t}\\int_{a}^{b}f(x,t)\\ \\mathrm{d}x=\\int_{a}^{b}\\frac{\\partial}{\\partial t}f(x,t)\\ \\mathrm{d}x$

结论：

如果函数 $f(x,t)$ 及其偏导数 $\\frac{\\partial}{\\partial t}f(x,t)$ 都在矩形区域 $[a,b]\ imes[m,n]$ 上连续，那么在 $[m,n]$ 上，以上等式成立。

证明：

设 $\\varphi\\left(t\\right)=\\int_{a}^{b}f(x,t)\\mathrm{d}x$

任取 $t_0\\in[m,n]$ ，取 $\\left| h \\right|$ 充分小，使得 $t_0+h \\in[m,n]$ ，于是有

$\\begin{align}\\frac{\\varphi(t_0+h)-\\varphi(t_0)}{h}&=\\frac{1}{h}\\int_{a}^{b}(f(x,t_0+h)-f(x,t_0))\\mathrm{d}x\\\\&=\\int_{a}^{b}\\frac{\\partial}{\\partial t}f(x,t_0+\ heta h)\\mathrm{d}x \\end{align}$

由于 $[a,b]\ imes[m,n]$ 为有界闭集，故 $\\frac{\\partial}{\\partial t}f(x,t)$ 在 $[a,b]\ imes[m,n]$ 上一致连续。

那么令 $h\\rightarrow 0$ ，即可得

$\\frac{\\mathrm{d}}{\\mathrm{d}t}\\varphi(t)=\\frac{\\mathrm{d}}{\\mathrm{d}t}\\int_{a}^{b}f(x,t)\\ \\mathrm{d}x=\\int_{a}^{b}\\frac{\\partial}{\\partial t}f(x,t)\\ \\mathrm{d}x$

来自常庚哲数学分析

上一篇：澳洲独立技术移民189申请要求，EOI打分和目前获邀分数，职业评估详解

下一篇：2021年三星手机怎么判断版本+最全区域产地代码表

粤IP*******