
如果你的日常开发工作对程序的运行性能敏感,你可能会有如下两个困惑:
- 我的程序中需要用到二维数组。 在 Fortran 中二维数组默认是列优先 (column-major),而 C/C++ 是行优先 (row-major),两种数据排布对程序性能到底有什么影响?
比如,我有一个 1024 x 512 大小的数组 a,在 C/C++ 中我到底应该是用 a[1024][512] 配上 a[i][j], 还是 a[512][1024] 配上 a[j][i] 来表示数据?
2. 我的程序中需要用到结构体的一维数组。 比如说,我有一个粒子系统,每个粒子有 x, y, z, w 四个属性。我应该采用 array of structure (AOS) 还是 structure of arrays (SOA) 的方式性能会更高?
具体来看,在 C++ 中,我应该用
// Array of structures (AOS)
struct Particle {float x, y, z, w};
Particle particles[1000];
还是
// Structure of arrays (SOA)
struct Particles {
float x[1000];
float y[1000];
float z[1000];
float w[1000];
};
?
这两个问题是数据排布的两个最核心的问题:行优先 v.s. 列优先 (row/column major),和 AOS v.s. SOA。
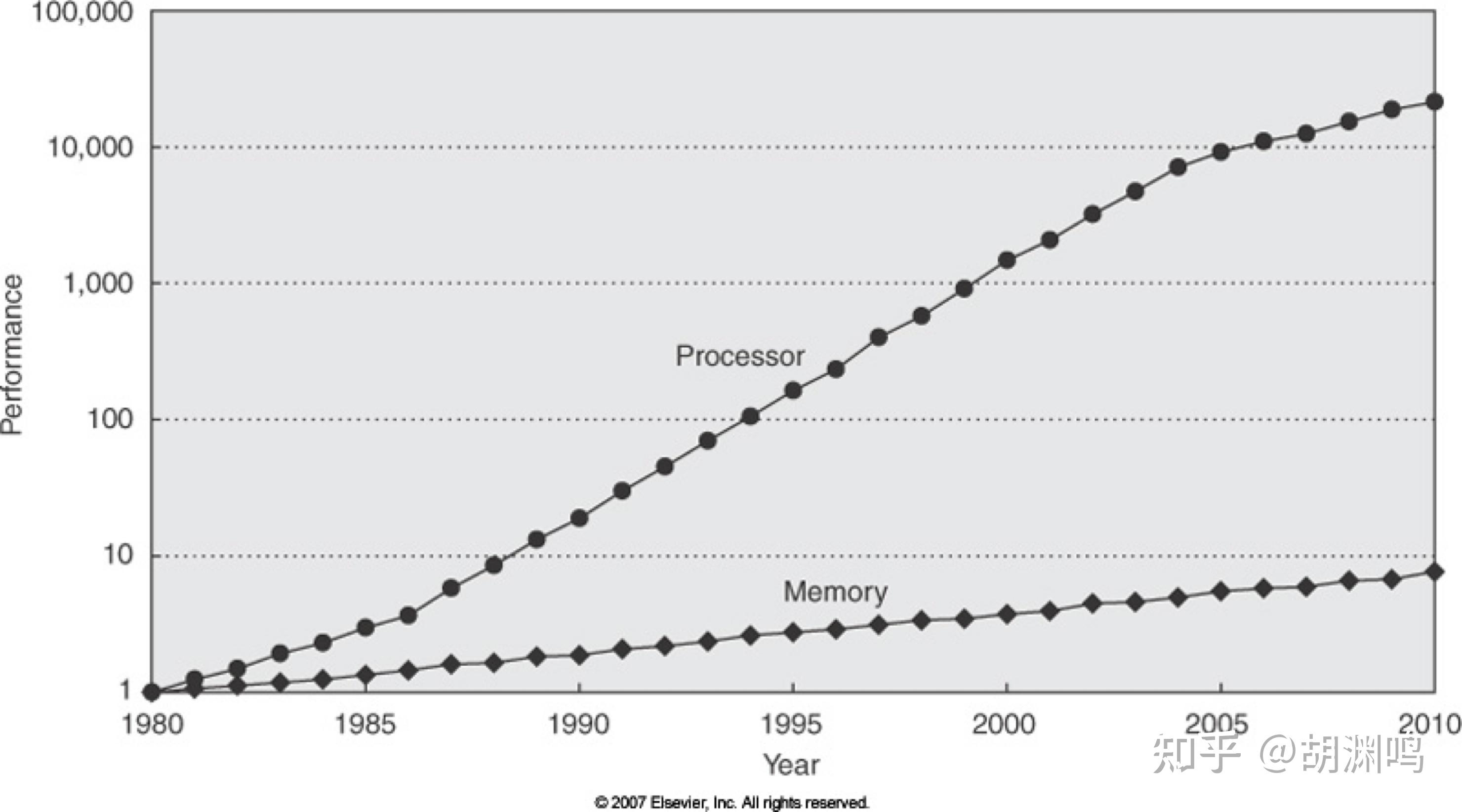
要是在三四十年前,或许程序的性能对于内存中的数据排布并不敏感。但是如今,由于 CPU/GPU 的计算吞吐量已经远大于主内存带宽,所以 访存经常成为比计算更需要优化的程序瓶颈。而数据排布方式直接决定了内存带宽利用率,优化程序的有效手段之一往往就是优化数据排布。
这篇文章就希望通过一系列实验来回答这两个问题。在相对专业的环境中,大家会用空间一致性 (spatial coherency)、内存层级(memory hierarchy)、Roofline model 等等理论体系来分析访存对于程序的影响。不同硬件的 cacheline、translation lookaside buffer(TLB)等属性也会影响最优的数据排布。这篇文章不会深入讨论这些问题,会用比较浅显的分析方式来考虑内存排布对于程序性能的影响。
当然,看完了这些,你可能还会有一个新问题:
3. 天哪,数据排布和性能的关系好复杂,我不想搞懂了,有没有什么办法可以让我不懂计算机底层也能轻松找到性能比较高的的内存布局?
答案是肯定的。我们的 Taichi 编程语言就针对这个情况做了设计,可以让你在只改动几个字符的情况下快速尝试不同的内存布局,迅速找到在不同硬件上的最佳布局方案。
在运行如下示例之前,请安装最新的 Taichi 1.1.0 版本,以下代码会用到 v1.1.0 的新特性。不管之前是否已经安装 Taichi,都可以用以下命令来安装、升级 Taichi:
pip install -U taichi由于篇幅限制,本文默认在 CPU 上讨论性能。虽然有些地方也会提到 GPU,但是不会深入讨论。
我们先来看行优先 v.s. 列优先这个问题。这里我们使用一个最基本的实例,给二维数组中的每一个元素赋值:
import taichi as ti
ti.init(arch=ti.cpu, kernel_profiler=True)
n = 4096
m = 4096
a = ti.field(dtype=ti.i32, shape=(n, m)) # 行优先(默认)
# a=ti.field(dtype=ti.i32, shape=(n, m), order='ij') # 行优先
# a=ti.field(dtype=ti.i32, shape=(n, m), order='ji') # 列优先
@ti.kernel
def foo():
for i in range(n):
for j in range(m):
a[i, j] = i + j
for repeat in range(100): # 运行 100 次用于评测
foo()
ti.profiler.print_kernel_profiler_info() # 打印 kernel 的时间占用在 Taichi 中,你可以修改 a=ti.field 的定义,来尝试各种数据布局。你可以使用 order='ij' 这样的语法来指定一个 field 的内存顺序。如果数组有更高维度,可以使用后续的字母,比如说 4维数组 可以使用 ijkl、lijk 这样的方式来指定。你可以运行几次上面的程序,来获取行优先、列优先模式下程序的性能。
上面这个程序在我的 M1 CPU 上,如果采用行优先(order='ij')运行时间为 6.3 ms,而列优先(order='ji')下运行时间为 36 ms,足足差了近六倍。
相对比较通用的结论是:内层循环相邻 iteration 访存地址应该尽可能接近。通常根据这个原则去排布数据能够得到较优的访存。 这是由缓存的结构决定的。这个原则被称为访存的空间局部性(spatial locality),也即相近的代码(指令)最好访问相邻的数据,这样硬件能够提供更好的性能。文章后半部分会通过 Cacheline 来讨论这类访存局部性的问题。
实际程序中的计算模式会比上述程序更加复杂一些。在 Taichi 中,可以通过 field 的 order 来指定数据布局方式,通过 Taichi 自带的 profiler 测试 kernel 性能,进行快速的调优。
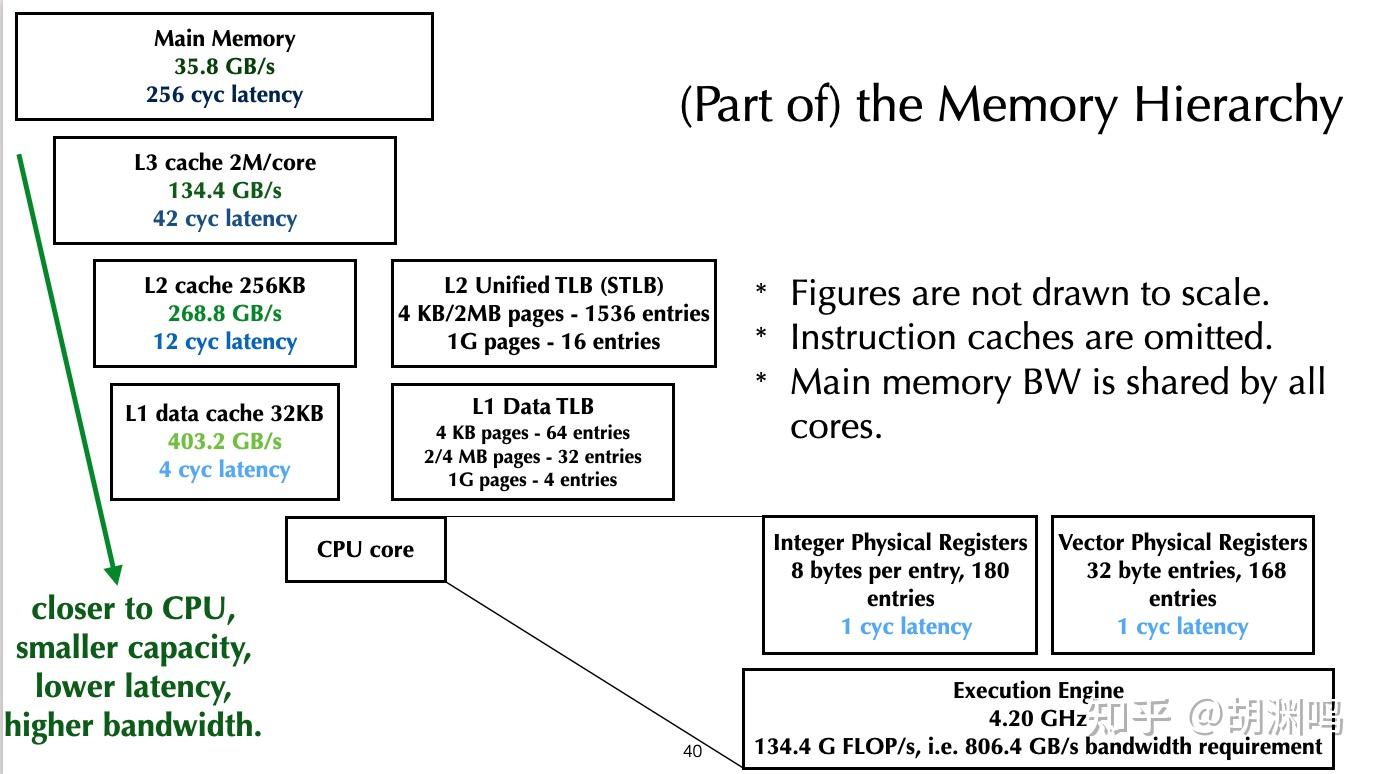
注:如果数组大小特别小,能够完全塞进 CPU 缓存(一般 L3 cache 是每个 core 有 1.5~2 MB,L2 是 256 KB,L1 是 32KB),那么或许排布对于性能的影响并不大。但是一旦数组规模超过 2MB 左右,就需要特别在意访存问题。
行优先、列优先的问题是一道开胃小菜,孰优孰劣通常也比较容易做出判断。下面我们来看一个更复杂一些的问题。
让我们考虑另一种问题:数组是一维的,但是每个元素中有多个成分。最常见的情况就是游戏或者物理仿真中的粒子系统,每个粒子有多个属性。对于这种问题,AOS、SOA 是两种最常见方式。
所谓 Array of structures (AOS),即同一个结构体(粒子)中的属性在内存中连续。在 C++ 中,可以这么表示:
// Array of structures
struct Particle {float x, y, z, w};
Particle particles[1000];
AOS 提供了较好的封装,比较接近大部分 C++ 程序员的思维,所以最常被使用。
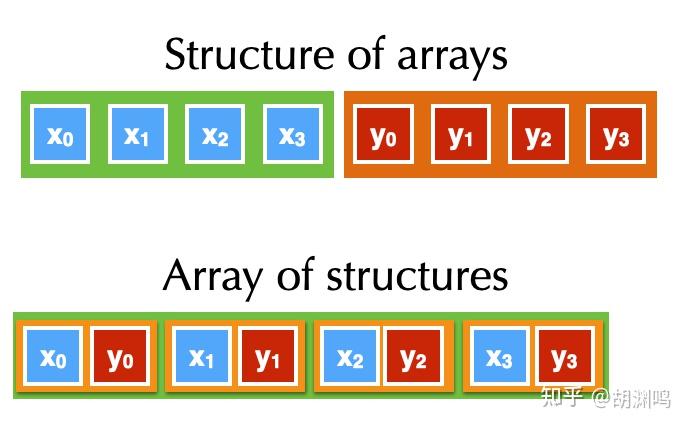
对于 Structure of array,就是另一个故事了。你需要用一种稍稍奇怪的方式来编写程序:
// Structure of arrays
struct Particles{
float x[1000];
float y[1000];
float z[1000];
float w[1000];
};这样的好处是一个属性(如 x)在不同结构体中的数据在内存中是连续的。这种写法看着比较奇怪,但是实际中有挺多好处:
- 如果有一些操作只用到属性的子集(比如说x, y, z 而没有 w),那么 SOA 的内存布局可以完全不浪费 w 造成的内存带宽。
注:这里要注意的是 CPU 上的 cacheline 大小是 64B、(NVIDIA) GPU 上是128 B,内存带宽的瓶颈往往是 last-level cache (LLC,比如 CPU 上的 L3 cache、GPU 上的 L2 cache) 到 main memory(也就是内存条)的 bandwidth。LLC 到 main memory 的单位是 cacheline (而不是 byte)。如果一个 cacheline 只用一部分,就会导致 main memory bandwidth 的浪费。在 AOS 的 data layout 下,由于一个粒子的 x, y, z, w 总是在同一个 cacheline 内,没有办法只向 main memory fetch 其中的一部分。后续的会有图片来说明这一点。
2. 在 GPU 上,SOA 能够发挥 GPU 硬件的 Coalescing 机制,硬件会把一个 warp (32 个 thread)的数据访问打包成一个 memory transaction,提高效率。类似地,在 CPU 上,SOA 对于 SIMD 模式的编程也更加友好(如 x86 架构下可以使用 _mm_load_ps 等 SIMD intrinsics 对数据进行向量化加载)。
3. SOA 的另一个好处是比较容易在运行时给一组数据添加一个 attribute,并且保持访问的高效。本文就不针对这一点展开了。
游戏中常用的 ECS 架构、Data-oriented design 模式(可以看一看知名游戏程序员 Mike Acton 2014 年在 CppCon 的经典 Talk)其实也和 SOA 有一些关系。
下面我们就通过一段 Taichi 程序来实地考察 AOS、SOA 对性能的影响:
import taichi as ti
ti.init(arch=ti.cpu, kernel_profiler=True)
n = 4 * 1024 * 1024
dim = 4
unroll = 8
a = ti.Vector.field(dim, dtype=ti.i32, shape=n,
layout=ti.Layout.AOS)
@ti.kernel
def assign_all():
for i in range(n):
for k in ti.static(range(dim)):
a[i][k] = i + k
@ti.kernel
def assign_all_unrolled():
for i_ in range(n // unroll):
for j in ti.static(range(unroll)):
i = i_ * unroll + j
for k in ti.static(range(dim)):
a[i][k] = i + k
@ti.kernel
def assign_single():
for i in range(n):
a[i][0] = i
@ti.kernel
def assign_single_unrolled():
for i_ in range(n // unroll):
for j in ti.static(range(unroll)):
i = i_ * unroll + j
a[i][0] = i
@ti.kernel
def assign_all_random():
for i_ in range(n):
for k in ti.static(range(dim)):
i = (i_ * 10007) & (n - 1) # Random index
a[i][k] = i + k
for repeat in range(30):
assign_all()
for repeat in range(30):
assign_all_unrolled()
for repeat in range(30):
assign_single()
for repeat in range(30):
assign_single_unrolled()
for repeat in range(30):
assign_all_random()
ti.profiler.print_kernel_profiler_info()稍微解释一下这个程序:我们开了 4 * 1024 * 1024 (4M)个 4D 向量的数组,占内存 64MB,超过了 M1 的 LLC 大小。assign_all 为整个数组中的所有内容赋值;assign_single 为所有向量的第 0 个分量(也就是 1/4 个数组的数据量)赋值;assign_all_random 类似 assign_all,但是采用随机访问的方式而不是顺序访问。除了这 3 个 kernel,我们还加上了 unroll 版本,让 kernel 在计算上跑的更快、对内存访问性能更加敏感。
我在我的 M1 CPU 上运行了这个程序(Taichi 会自动并行顶层的 for loop),可以得到以下的结果:
| Time (ms) | assign_all | assign_all_unrolled | assign_single | assign_single_unrolled | assign_all_random |
|---|---|---|---|---|---|
| AOS | 2.408 | 2.293 | 2.375 | 1.988 | 18.662 |
| SOA | 2.483 | 2.311 | 1.663 | 0.450 | 35.275 |
通过数据,有一些有趣的发现:
1. 不论是何种布局,顺序访问都比随机访问快。
2. 对于这种轻量级的计算,loop unrolling 有明显的加速。原因也很明显:通过 loop unrool,循环体本身的指令开销被充分均摊,访存瓶颈更加明显,对于内存排布也就更加敏感。
3. 我们专注于比较 unroll 以后的程序的性能。当需要填充整个数组的时候,AOS 和 SOA 布局差异不大,2.293 v.s. 1.988,差异在 15% 以内。
4. 当只需要填充每个向量的第一个分量的时候(也就是 1/4 个数组),SOA 布局只需要 AOS 布局 1/4 的时间。
结论 3 或许还在意料中,但是结论 4 就很有意思。通过 cacheline 来分析特别容易:对于结论 4 中的 AOS 布局,虽然 assign_single_unrolled 只用到了 1/4 的数据,但是并没有跳过任何 cacheline。每个 64B 的 cacheline 只有 4 * 4=16 B 被用到了,剩下的 48B 完全浪费了。而 SOA 的布局则确确实实只会访问 1/4 的 cacheline,所以性能更高。
SOA 一定永远比 AOS 好吗?还真不一定。
- 如果你的访问是顺序访问,那么 SOA 通常比 AOS 效率高一些。特别是当你的程序在 GPU 上运行的时候,因为 Coalescing。
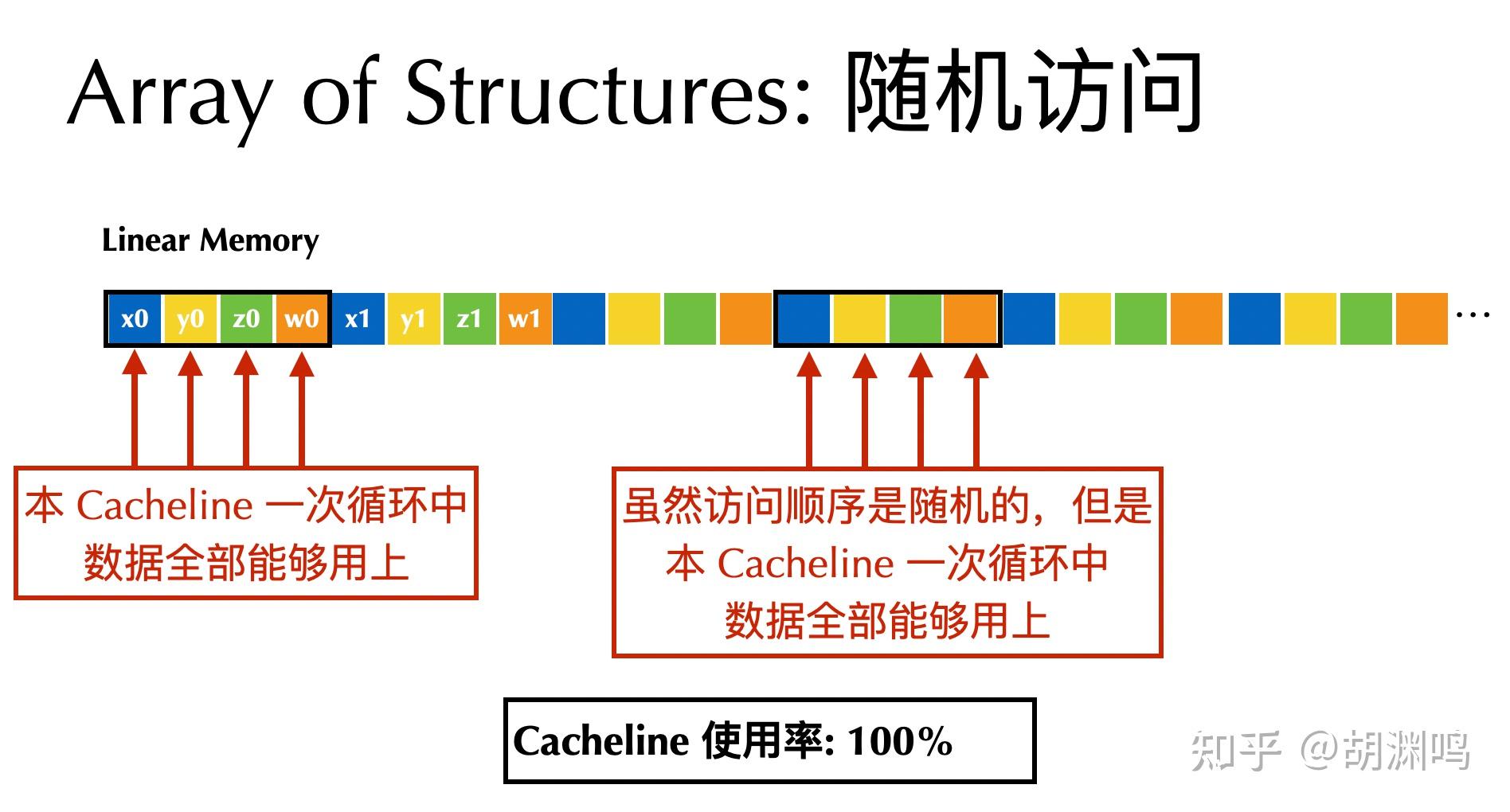
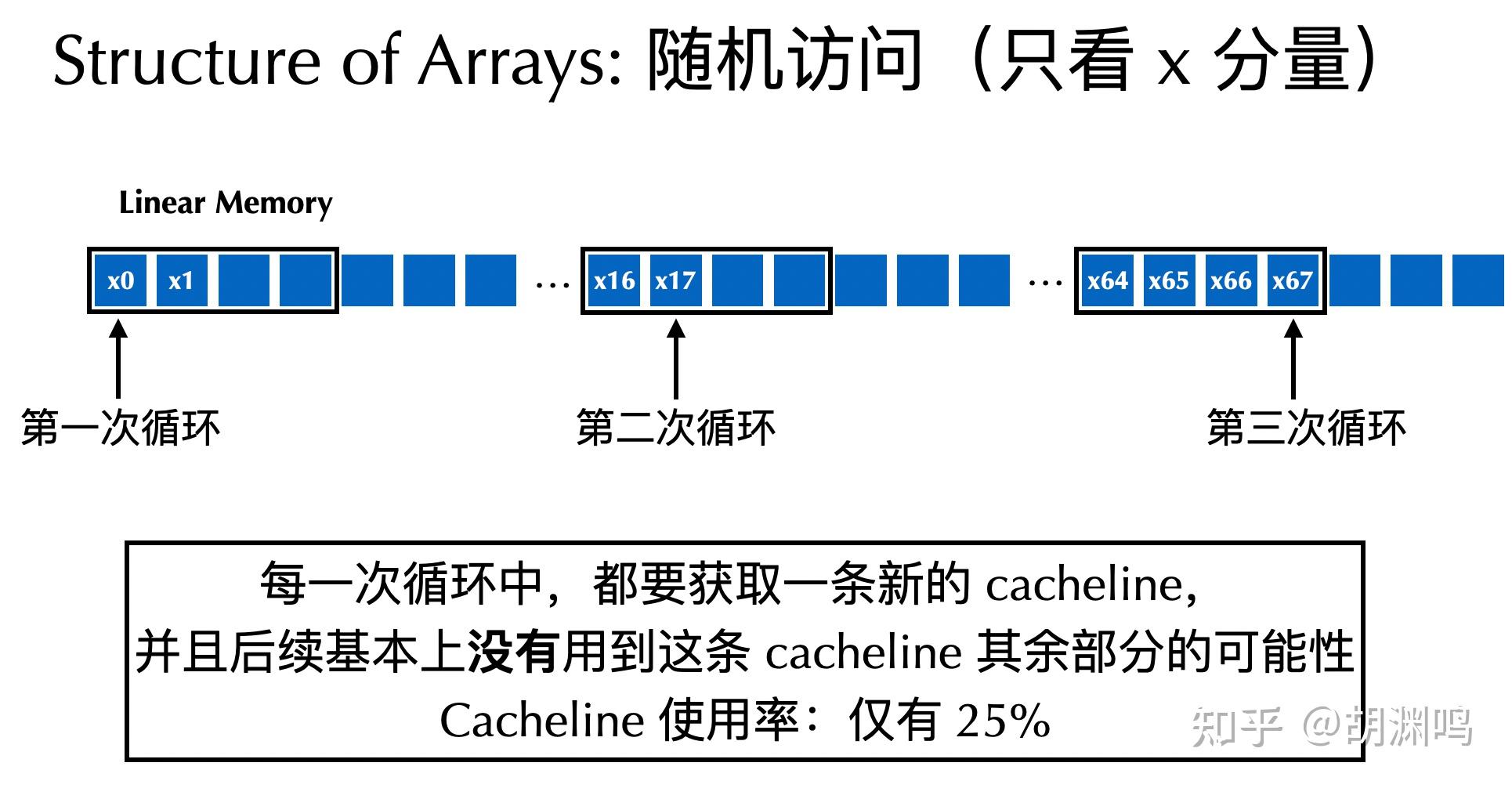
- 如果你的访问是随机访问,那么 AOS 常常比 SOA 更好。因为随机访问的一个粒子的数据在 AOS 下是在同一个 cacheline 中,而在 SOA 布局下会分散在 4 个 cachelines 里面,对于 AOS 的 cacheline utilization(缓存行利用率)会高很多。比如在上面的例子中,
assign_all_random在 AOS 布局下就比 SOA 快了近 2 倍。欢迎感兴趣的读者从 cacheline 的角度进行分析。下面的两个图也许能够帮助理解:
实际情况中,往往还会有更加复杂的内存布局,比如 Array of structures of arrays (AOSOA) 等,Taichi 通过 SNode 系统也可以支持,感兴趣的同学可以阅读文档(中文,英文),这里不再深入讨论。
需要注意的是,如果你的程序并不是用相对接近机器的语言编写(比如说未经过 Taichi 加速的 Python、Ruby 等语言),那么可能解释器开销才是性能瓶颈。这种情况下优化内存排布帮助就不会很大了。而对于 C、C++、CUDA、Javascript、GLSL、Taichi 等相对高性能的语言,并且计算任务需要大量访存时,优化内存布局价值就会较大。
另外还需要判断程序到底是 compute bound 还是 memory bound。比如,在第一个程序中,如果
a[i, j] = i + j被换成
a[i, j] = ti.sin(i + j)那么在 CPU 上这个程序的瓶颈就会变成三角函数 sin 的计算(一次要十几甚至即使几十个时钟周期),而内存访问效率的重要性就没有那么重要了。
常常被忽视的一点是,要先找到性能瓶颈,再进行优化。如果一段代码只占程序运行时间的 1%,那么即使你的代码优化到极致,也只能将程序运行时间减少 1%。
有时一些比较简单的方式也能优化程序性能。比如说,你的数据是否可以分成两部分,(在两台机器上)开两个程序运行,然后再合并数据?这对于“批量处理一万张图片”这样以文件为输入单位的情况往往非常有效。
现在问题来了,如果你有一个 3D 数组,那么光是排列顺序就会有 ijk、ikj、jik、jki、kij、kji 六种,如果数组中的元素还是向量,那么又会有选择 AOS、SOA 的问题,于是就出现了 12 种选择。很多时候,面向高性能计算的程序员还会使用 blocking、tiling 等等技巧,有时还会配上 Morton coding,出现各种各样的神奇排布方案。以上讨论还只局限于 CPU。在 GPU 上很多结论有会变成另外一个故事了(需要考虑 coalescing 等等机制)。即使是最有经验的程序员,往往也需要通过实验的方法来确定最佳内存布局。
如果使用 C++ 等语言,改变内存布局相对比较麻烦,因为 C++ 内置的数组结构其实只有固定的一种 order,那就是 ijkl 这样的顺序 order。切换 AOS、SOA 往往也会涉及到软件架构上的调整。
好消息是,在 Taichi 中,可以通过 ti.field(order='ijk', layout=ti.Layout.AOS/SOA) 中的 order、layout 两个参数来快速调整数据布局,而不必改变任何计算程序(即 ti.kernel 中的内容)。对于 Taichi 中的 vector/matrix field,可以同时测试两个参数的组合。
Taichi 实现了数据布局和计算的解耦,使得尝试一种新的数据布局的成本很低,往往只需要改几个字符。 于是,在很多 Taichi 程序中,要寻找一种较优的数据布局的方式很简单:设立性能 benchmark,然后快速尝试!
欢迎大家尝试在已有的 Taichi 程序中调整数据布局,观察程序的性能变化 :-)
限于篇幅这篇文章没有深入探讨原理,更多是给读者一种直观的印象:什么样的内存布局在什么情况下性能更高。欢迎大家留言,如果大家感兴趣的话,后面我再写一篇更深入讨论这些问题内在原理的文章。另外,在第一个实验中也没有深入讨论为什么行优先、列优先会有性能差异。大家也可以自己借助 cache 的性质进行分析和学习。
最后,欢迎大家来参加 Taichi 社区的数值计算兴趣小组活动,今晚 8 点会由我来分享一些高性能计算基础知识:
直播链接:Bilibili
内容安排信息:https://forum.taichi.graphics/t/sig-03/2845

如果想一键体验 Taichi,只需要执行
pip install -U taichi并执行
ti gallery就可以体验各种基于 Taichi 的高性能可视化 Demo:

- 更多内容:



