Lingo是一款求解最优化问题的软件，可以用于求解非线性规划，也可以用于一些线性和非线性方程组的求解等，功能十分强大，是求解优化模型的最佳选择。

首先介绍一下什么是最优化问题。

最优化问题，即在所有可行的方案中选出使得目标最优的方案的实际问题。

优化问题的三要素是：

• 决策变量
• 约束条件
• 目标函数

根据决策变量取值情况不同，分为连续型和离散型。

根据有无约束条件分为无约束优化和带约束优化。

根据处理思想方法不同，分为数学规划（函数优化问题）、组合优化、图论与网络流、动态规划、目标优化、模糊优化、随机优化、对策与决策……

求解这样一个问题，只需直接输入如下代码，写法基本与数学公式一直，不用改写成标准形式

min=2*x1+3*x2;
x1+x2>=350;
x1>=100;
2*x1+x2<=600;

点击 图标运行：

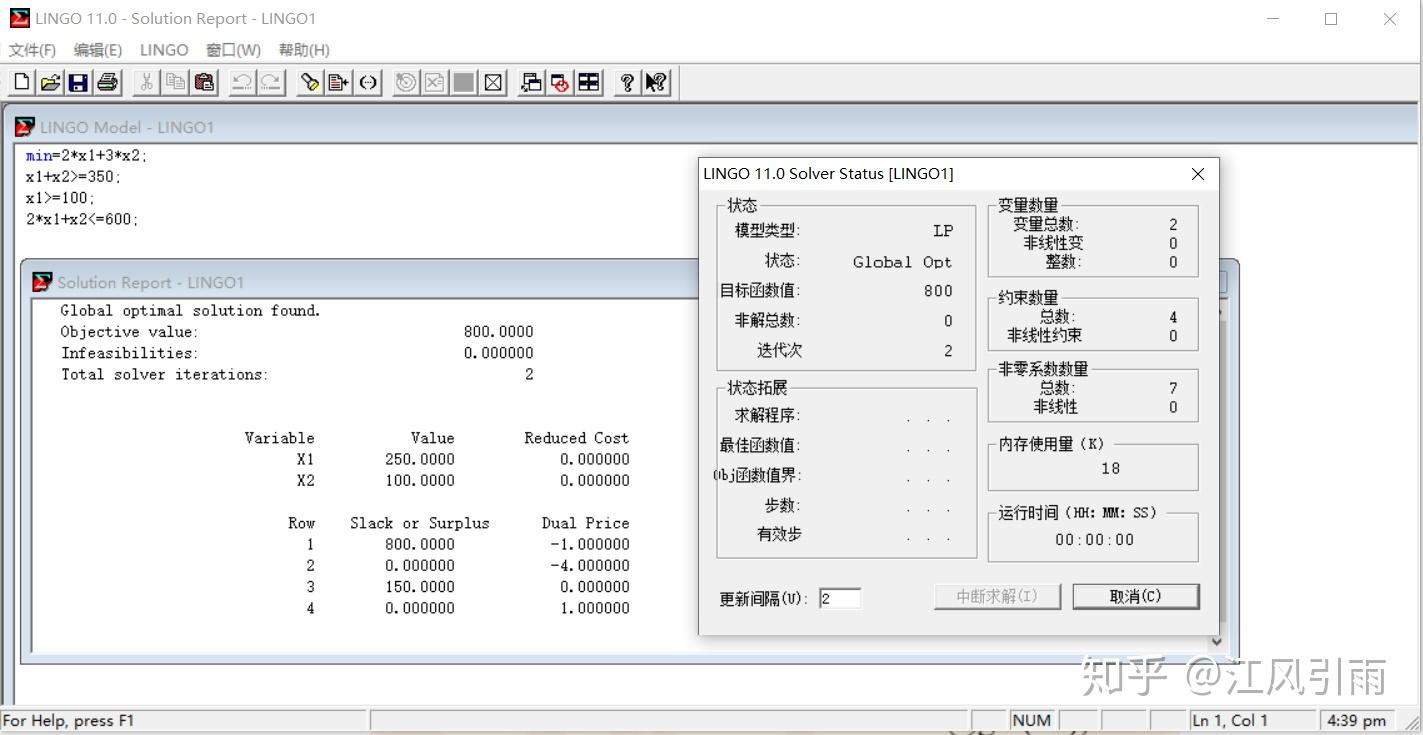
可以看到直接识别出了问题类型，并找到了全局最优解。

@free: 可正可负（默认大于等于0）
@gin：整数

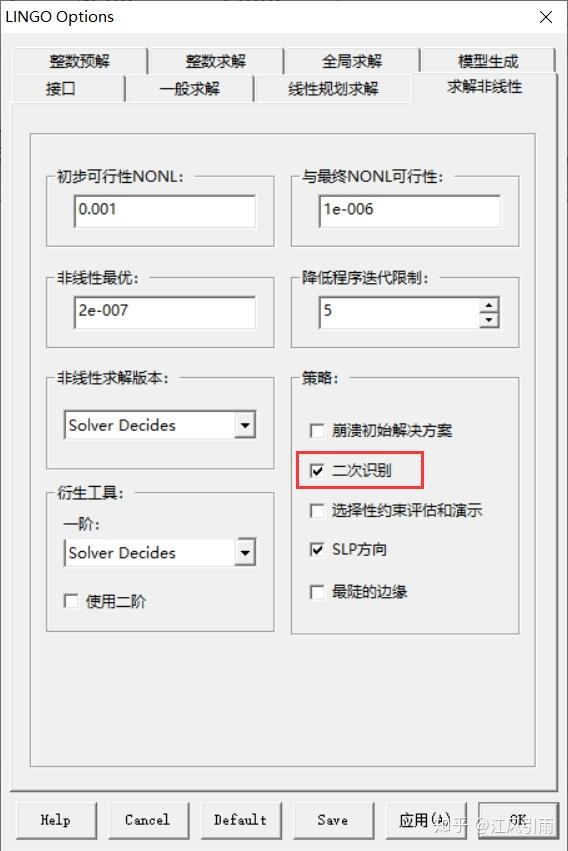
?一定要在Lingo选项->求解非线性菜单中勾选二次规划识别！！否则会按照INLP问题求解,只能得出局部最优解。

max=98*x1+277*x2-x1^2-0.3*x1*x2-2*x2^2;
x1+x2<=100;
x1<2*x2;
@gin(x1);@gin(x2);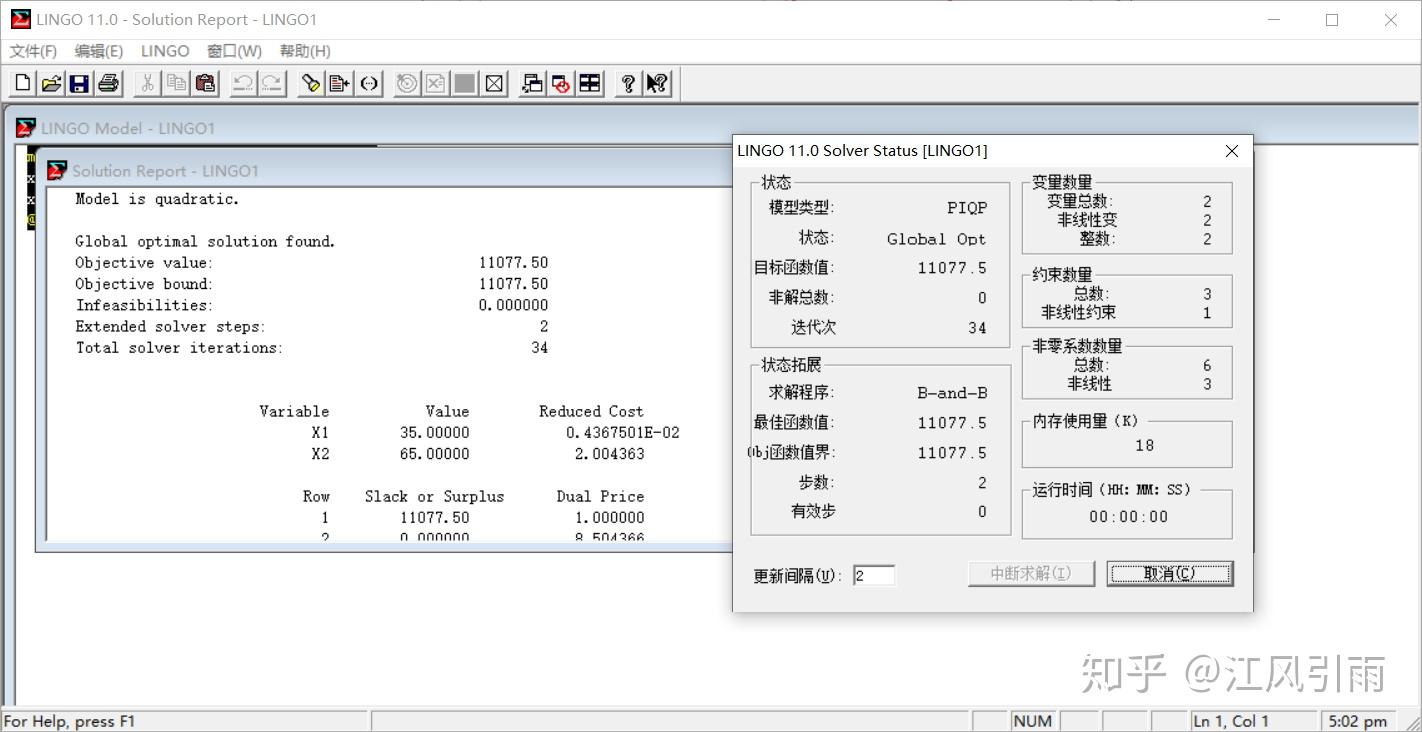

• 算数运算符 + - * / ^
• 关系运算符 <(=)=>(=)
• 逻辑运算符
• 否定 #NOT#
• 相等 #EQ#
• 不等 #NE#
• 与 #AND#
• 或 #OR#
• 大于 #GT#
• 大于等于 #GE#
• 小于等于 #LE#
• 小于 #LT#

• @ABS(x) 绝对值
• @SIN(x)，@COS(x) ... 三角函数
• @EXP(x) 返回
  
• @LOG(x) 自然对数
  
• @SIGN(x) x<0返回-1；否则返回1
• @FLOOR(x) 返回x靠近0的整数部分，如@FLOOR(1.2)=1,@FLOOR(-2.3)=-2

• @pbn(p,n,x) 二项分布
• @pcx(n,x) 卡方分布
• @pfd(n,d,x) F分布
• ……

Lingo变量默认是非负的

• @bin(x) x=0或1
• @bnd(L,x,U)
  
• free(x) 实数
  
• @gin(x) 整数

@IF(logical_condition,true_result,false_result)

例：分段函数

f\\left( x \\right)=\\begin{cases}100,x>0\\ 2x, x\\le 0\\ \\end{cases}

fx=@if(x #gt# 0,100,2*x)

• @in(set_name,index_1[,index_2]) 是否在集合中，返回0/1
• @wrap(index,limit) 取模，返回 j=index-k*limit=index(mod limit) +1, k为整数，保证j在[1, limit]内
• @size(set_name) 集合成员个数

• @FOR(set_name:constraint_expressions) 对每个元素生成约束
• @MAX(set_name:expressions) 表达式的最大值
• @MIN(set_name:expressions) 表达式的最小值
• @SUM(set_name:expressions) 表达式的和

例：产生序列{1，4，9，16，25}
model: sets: number/1..5/:x; endsets @for(number(i):x(i)=i^2); end
例：
matlab s=@sum(number(i)|i#le# 5: x); !前5个求和 m=@min(number(i)|i#ge# 5: x); !5个之后的最小值

• @OLE excel表格读取
• @file
• @text

• @status()
• 0 Global Optimum 全局最优
• 1 Infeasible 不可行
• 2 Unbounded 无界
• 3 Undetermined 不确定
• 4 Feasible 可行
• 5 Infeasible or Unbounded
• 6 Local Optimum 局部最优
• 7 Locally Infeasible 局部不可行（可行解可能存在，但lingo没找到）
• 8 Cutoff 目标函数的截断值被达到
• 9 Numeric Error 算数错误

• 尽量使用实数优化，减少整数约束和整数变量
• 尽量使用光滑优化，少用绝对值、符号函数、多变量求最大/最小值、四舍五入、取整等
• 尽量使用线性模型，x/y<5改为x<5y
• 合理设置上下界，尽可能给出变量初始值
• 参数数量级适当，不同参数数量级差距一般要求小于3

原文地址：

ps. 知乎的markdown支持也太差了吧，公式识别不了，图片屡屡上传失败，这点真该跟隔壁csdn学学