文章连接：https://doi.org/10.1016/j.cossms.2020.100853

近日，南京大学陈延峰教授研究团队和密歇根大学毛晓明教授课题组成员合作在期刊《Current Opinion in Solid State & Materials Science》上发表综述文章“Topological mechanical metamaterials: A brief review”，回顾了近年来拓扑机械超构材料的最新研究进展，论文第一作者为南京大学李鑫副研究员，通讯作者为南京大学卢明辉教授和陈延锋教授，南京大学的余思远副教授及密歇根大学的Liu Harry博士亦对本文的撰写有重要贡献。
研究背景

在Thouless，Haldane和Kosterlitz等人提出了物质拓扑相与相变理论之后，人们研究了大量具有相变、对称性和非平庸拓扑性质的新型拓扑材料，从自然存在的电子材料到人工基元组成的电磁、声学超材料等等。而在经典机械系统中实现非平庸拓扑性质的研究则是在近几年才受到研究人员的关注。其独特的拓扑特性提供了常规力学超构材料难以实现的应用前景，例如实现机械波的单向无损传输、实现振动隔离、构建具有抗破坏的畴结构，甚至提供具有鲁棒性的信息传输及存储等等。

我们知道，量子力学与经典力学的基本方程分别为薛定谔方程和牛顿方程，两者似乎没有直接关联。为了在经典力学中实现拓扑相，我们考虑一组经典的弹簧质量系统的运动，并将其看成一个典型的频率为ω 的Hermitian特征值问题，那么牛顿方程则可以写成如下形式：

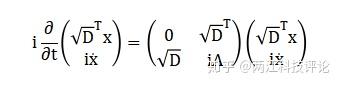
显然，该方程具有薛定谔方程的形式，使得这一经典力学系统具有了类似超导体中的粒子-空穴对称性，从而为经典力学系统中实现拓扑相提供了条件。

针对上述方程，本文分别回顾了准静态自由运动（ω=0）和有限频率（ω ≠ 0）系统中的拓扑相研究，包括拓扑Maxwell晶格，折纸/剪纸结构，以及在机械系统中实现固体弹性波的量子霍尔效应、谷霍尔效应等等。

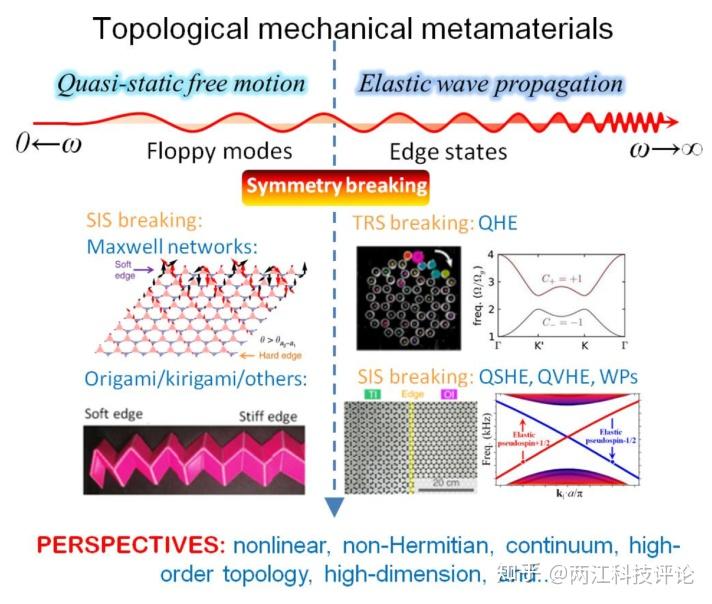
研究进展

（1）有限频率（ω ≠ 0）的弹性波系统

类似于空气声波，要在固体弹性波系统中实现拓扑性质（拓扑边界态），可以通过打破系统的时间反演对称性（Time reversal symmetry）或者空间反演对称性（Space inversion symmetry）来实现。这一部分回顾了如何在机械系统实现类量子霍尔效应、量子自旋霍尔效应、谷霍尔效应以及外尔半金属。

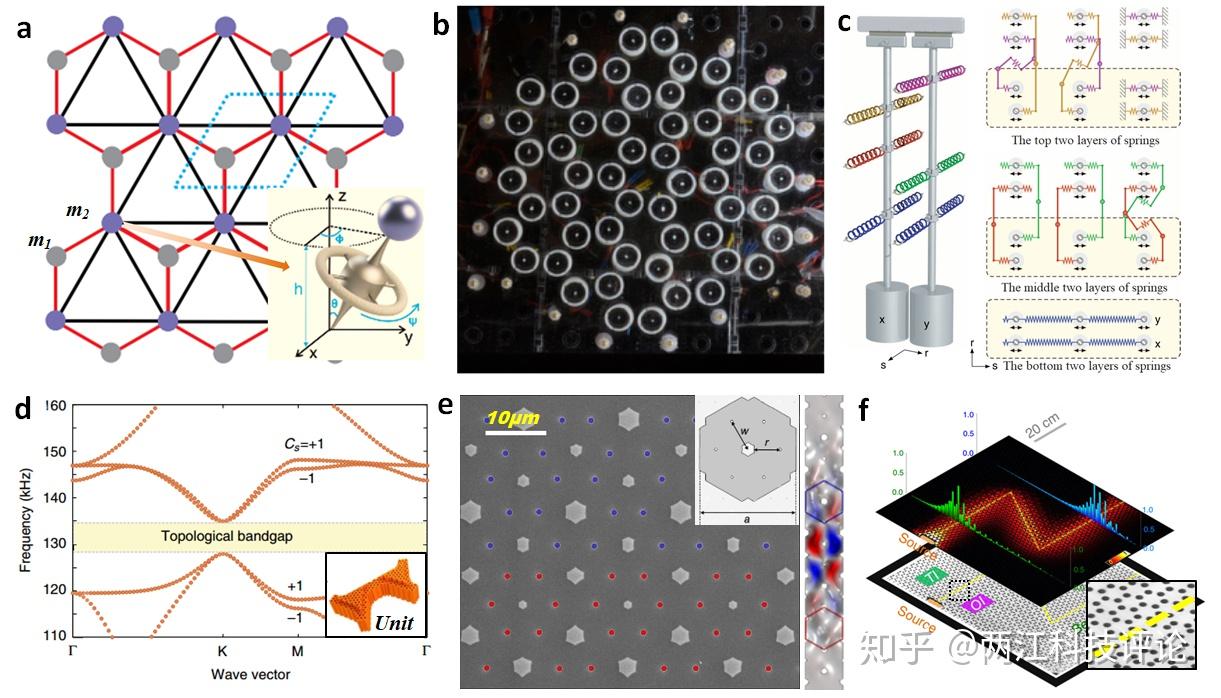
图2 a,b) 利用陀螺仪转动打破时间反演对称性实现弹性波类量子霍尔效应。c,d,e,f) 利用机械振荡器系统、多尺度蜂窝板、蜂窝晶格以及穿孔板构建弹性波赝自旋，从而实现弹性波类量子自旋霍尔效应。

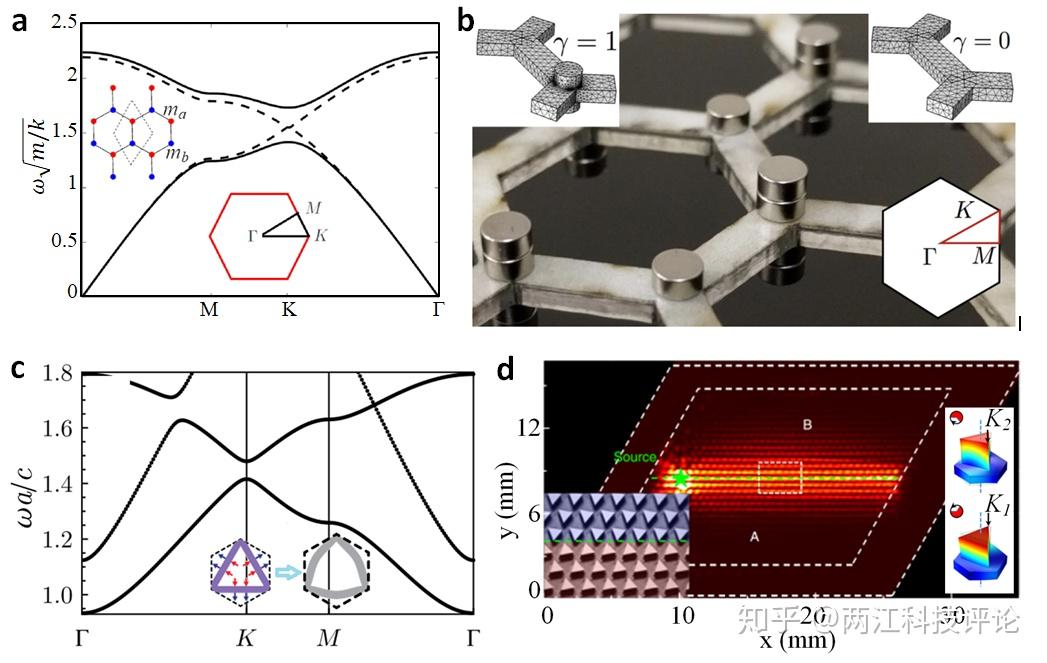
图3 通过改变蜂窝晶格点质量（a,b）、引入应变/力场(c)、精确排列三角柱谐振阵列(d)等方式打破空间反演对称性，从而实现弹性波类谷霍尔效应。

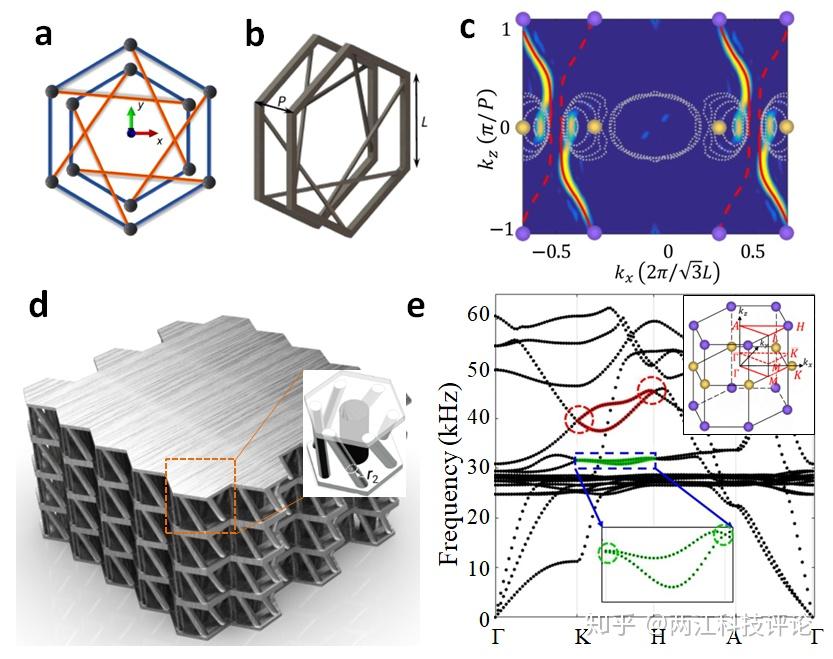
图4 利用手性连杆连接二维蜂窝形成三维结构，在三维空间形成弹性波外尔点(Weyl point)，从而实现三维弹性波拓扑相。

（2）准静态自由运动（ω=0）的机械系统

在准静态机械系统中实现拓扑性质相同样需要打破系统的空间反演对称性，涉及到系统的松散模式（Floppy Mode，Soft Mode 或Zero Mode），自应力状态（State of Self-Stress）以及畴壁（Domain Wall）等。这一部分首先介绍了如何在力学SSH模型中实现拓扑边界态，进而扩展到Maxwell晶格以及Maxwell网络，同时介绍了一些特殊准静态机械系统中的拓扑相，如折纸结构、鱼骨结构、M?bius环等。

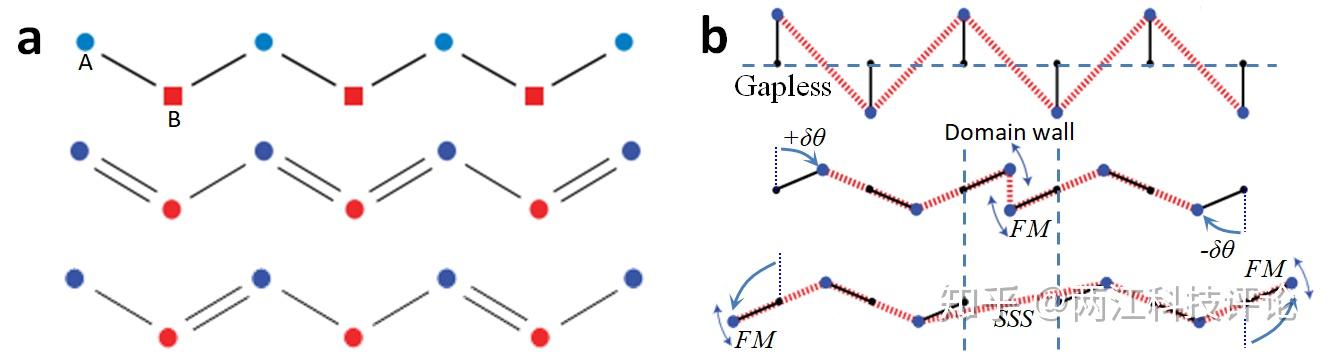
图5 力学“SSH”模型中的畴壁、松散模式、自应力状态的实现方式。

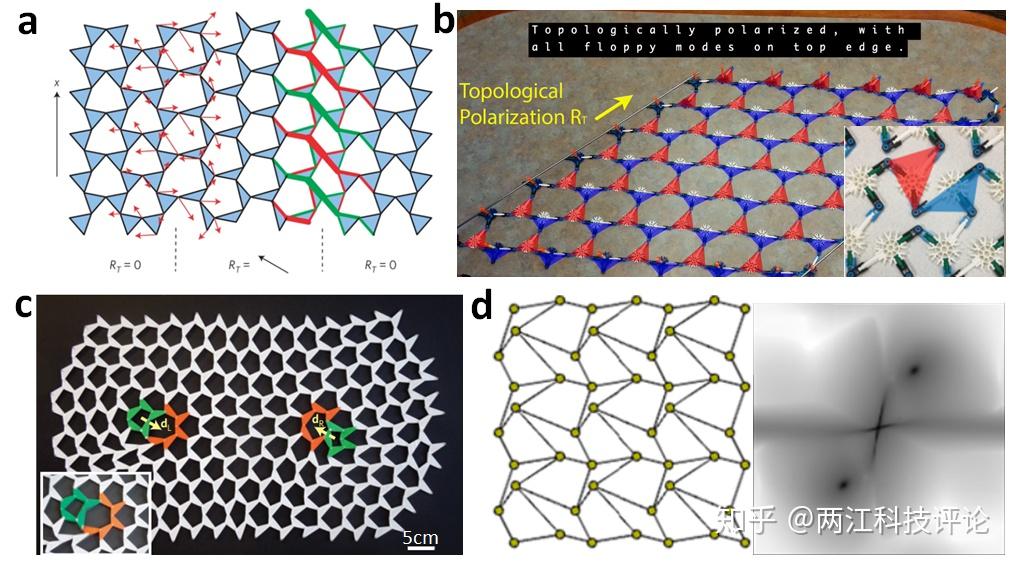
图6 利用晶格排列打破空间反演对称性，产生不同晶格矢量，从而建立拓扑极化（Topological polarization），进而在Maxwell晶格中实现拓扑相。

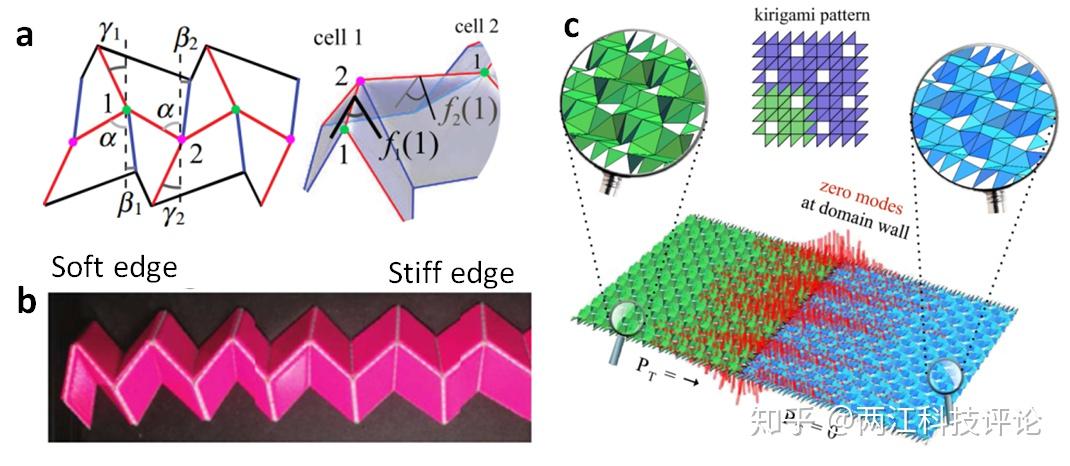
图7 a, b)通过精确设计的折痕在折纸结构中实现类SSH模型，c)通过移除折纸中的某些单元实现折纸结构的拓扑极化，产生具有松散模式的畴壁。

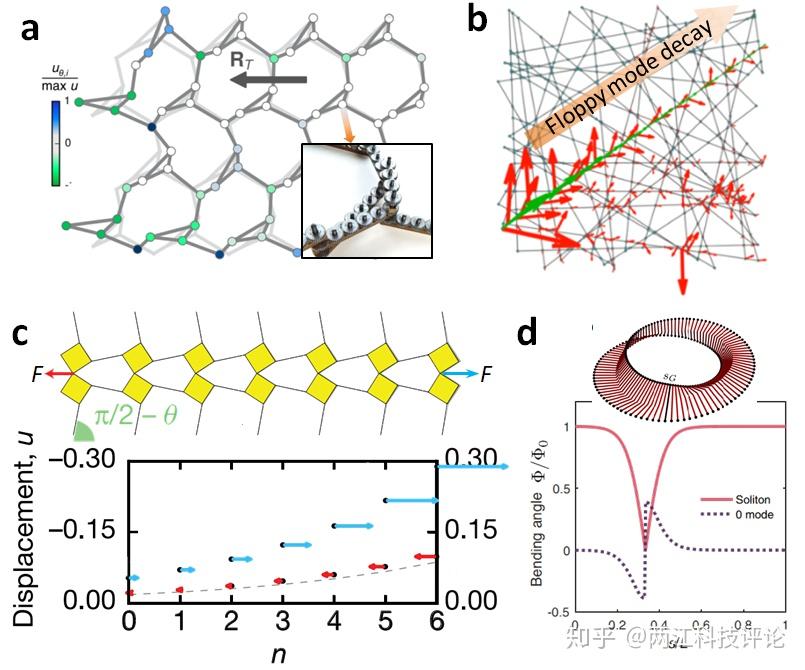
图8 机械系统中的Martini晶格(a), 无序纤维网络(b)，鱼骨结构(c)以及M?bius环(d)中的拓扑相。

展望

目前机械系统中拓扑态的研究大多局限于一维或者二维的线性系统，仍有许多未知的现象、机制以及应用有待探索。例如如何在非线性、非厄米机械系统中实现拓扑态等。此外，近期对于高阶拓扑绝缘体的研究以及无定形系统中拓扑相的研究也十分有利于在经典机械系统中实现相关应用。对于三维机械系统而言，其拓扑态的实现比二维系统更为困难，一个根本原因在于三维机械系统中不同模式间具有更为复杂的相互作用及耦合，对这类系统拓扑态的研究目前尚待深入开展。相信随着拓扑物理及材料研究的深入以及超高精度制造技术的持续发展，将会涌现出更多新颖的拓扑机械超构材料，并得以在工程领域得到广泛应用。

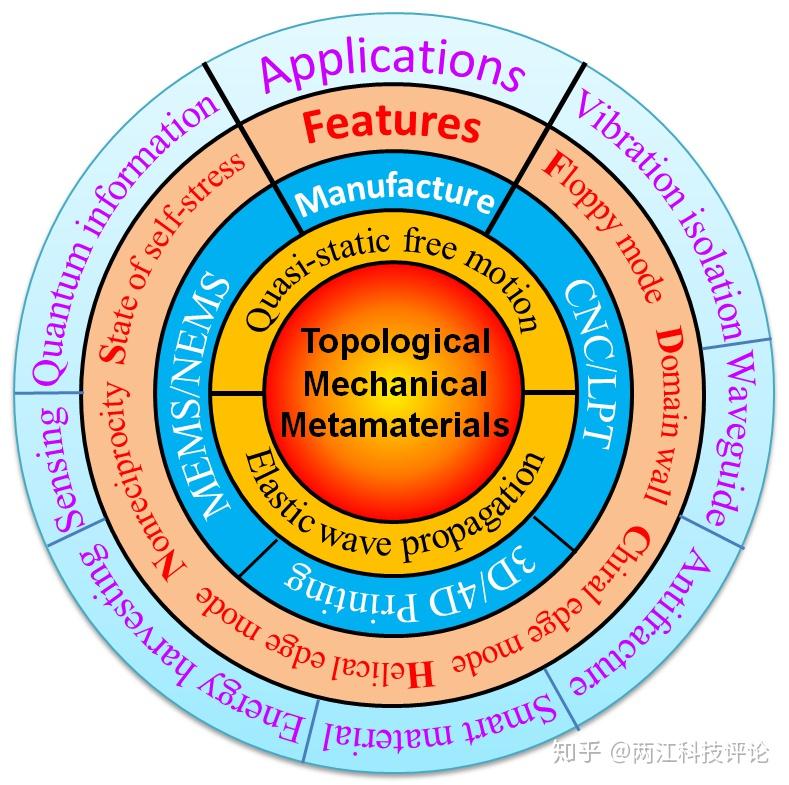
图9 拓扑机械超构材料特性、制造及应用

免责声明：本文旨在传递更多科研资讯及分享，所有其他媒、网来源均注明出处，如涉及版权问题，请作者第一时间后台联系，我们将协调进行处理（按照法规支付稿费或立即删除），所有来稿作者文责自负，两江仅致力于搭建优异的分享平台。转载请注明出处，如原创内容转载需授权，请联系025-85890989。