
- 一阶优化算法
- 梯度下降,负梯度方向上移动可以减小 f
- 二阶优化算法
- 二阶优化算法使用了二阶导数(也叫做Hessian方法)来最小化或最大化损失函数。由于二阶导数的计算成本很高,所以这种方法并没有广泛使用
- 大多数深度学习算法涉及某种形式的优化。
- 优化指的是改变 x 以最小化或最大 化某个函数 f(x) 的任务。我们通常以最小化 f(x) 指代大多数最优化问题。
- 最大化 可经由最小化算法最小化 ?f(x) 来实现
- 导数 f′(x) 代表 f(x) 在点 x 处的斜率。
- 它表明如何缩放输入的小变化才能在输出获得相应的变化:f(x + ε) ≈ f(x) + εf′(x)。
- 导数对于最小化一个函数很有用,因为它告诉我们如何更改 x 来略微地改 善 y 。
- 我们知道对于足够小的 ε 来说,f(x ? εsign(f′(x))) 是比 f(x) 小的,=f(x)-εf′(x)*sign(f′(x) 恒为负,sign x>=0,y=1, x<0, y=-1
- 负梯度方向减少函数值
- 使 f 下降得最快的方向 ,min ||u||||?xf(x)|| cos, 这在 u 与梯度方向相反时取得最小。
- 针对多维输入的函数,有偏导数的概念,针对xi, X处只有xi增加时,f(x)如何变化。
- 在单位向量u上的方向导数是 函数 f 在 u 方向 的斜率,方向导数是函数 f (x + αu) 关于 α 的导数(在 α=0 时取得)。
- 梯度向量指向上坡, 负梯度向量指向下坡。我们在负梯度方向上移动可以减小 f
- x′=x ? ε?xf(x)
- 梯度下降最小化损失函数,在神经网络模型中进行权重更新,即在一个方向上更新和调整模型的参数
- θ=θ?η×?(θ).J(θ)?是损失函数,其中η是学习率,?(θ)是损失函数J(θ)的梯度
批量梯度下降将计算整个数据集梯度,但只会进行一次更新
- 缺点
- 因此在处理大型数据集时速度很慢且难以控制,甚至导致内存溢出
- 优点
- 当目标函数为凸函数时,BGD一定能够得到全局最优,
- 方便的数据并行
随机梯度下降是每次迭代使用一个样本来对参数进行更新。使得训练速度加快
- 缺点:
- 准确度下降
- 由于即使在目标函数为强凸函数的情况下,SGD仍旧无法做到线性收敛可能会收敛到局部最优
- 由于单个样本并不能代表全体样本的趋势不易于并行实现
- 优点:
- 由于不是在全部训练数据上的损失函数,而是在每轮迭代中,随机优化某一条训练数据上的损失函数,这样每一轮参数的更新速度大大加快
每次迭代选取k个样本来进行参数更新
- 缺点
- batch_size的不当选择可能会带来一些问题。
- 优点
- 通过矩阵运算,每次在一个batch上优化神经网络参数并不会比单个数据慢太多。
- 每次使用一个batch可以大大减小收敛所需要的迭代次数,同时可以使收敛到的结果更加接近梯度下降的效果。
- 可实现并行化。
鞍点的定义: 鞍点在所有维度的
梯度是 0,但是在一些维 度上是最高点,在另一些维度上是最低点
- 利用Hessian矩阵,判断是否为鞍点,因为,Hessian在鞍点具有正负特征值,而在局部最小值点正定。
- 随机梯度,相当于给正确的梯度加了一点noise,一定程度上避免了鞍点
- 在梯度方向上引入随机性
最优化问题之如何逃离(跳出)鞍点(Saddle Points)最优化问题之如何逃离(跳出)鞍点(Saddle Points)
其实应该 动量法 Momentum , NAG , adam算法, AdaGrad、RMSprop、AdaDelta
都可以解决鞍点问题。
- 很难选择出合适的学习率
- 相同的学习率并不适用于所有的参数更新: AdaGrad、RMSprop、AdaDelta
- 高维空间如何逃离鞍点
动量法:上个步骤中更新向量的分量’γ’添加到当前更新向量 V(t)=γV(t?1)+η?(θ)J(θ)
- 优点:使网络能更优和更稳定的收敛减少振荡过程
- 缺点:容易错过最小值,到达最低点时动量太高,从而错过
Nesterov梯度加速法:先根据之前的动量进行大步跳跃,然后计算梯度进行校正
V(t)=γV(t?1)+η?(θ)J( θ?γV(t?1) ),然后使用θ=θ?V(t)来更新参数。
- 优点:这种预更新方法能防止大幅振荡,不会错过最小值,并对参数更新更加敏感
Adagrad:每个参数的维度上收敛速度都不相同,因此根据不同参数的收敛情况分别设置 学习率 ,
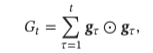
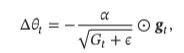
- 优点:不需要手工来调整学习率,
- 缺点:累计分母会越来越大,系数会越来越小,学习率会越来越小,很难找到最优点了
RMSprop: 解决adagrad的问题,由累计方式变成移动平均在迭代过程中,每个参数的学习率并不是呈 衰减趋势,既可以变小也可以变大
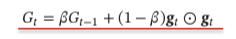
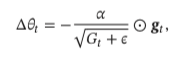
- 优点: 可以在有些情况下避免 AdaGrad 算法中学习率不断单调下降以至 于过早衰减的缺点.
adam: 计算了每个参数的对应学习率,还计算每个参数的对应动量变化并独立存储
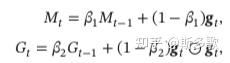

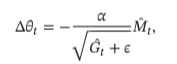
- 优点:与其他自适应学习率算法相比,其收敛速度更快,学习效果更为有效,而且可以纠正其他优化技术中存在的问题,如学习率消失、收敛过慢或是高方差的参数更新导致损失函数波动较大等问题
- 缺点:Adam在某些情况下可能会不收敛
adamw: 因为L2正则化和weight decay 在adam上不等价,Adam优化带L2正则的损失并不有效:
- 正常的权重衰减是对所有的权重都采用相同的系数进行更新,本身比较大的一些权重对应的梯度也会比较大,惩罚也越大。
- 但由于Adam计算步骤中减去项会有除以梯度平方的累积,使得梯度大的减去项偏小,从而具有大梯度的权重不会像解耦权重衰减那样得到正则化
adamw的改进:将衰减值,放到最后的位置,使用相同的λ \\lambdaλ来正则化所有的权重,完成了梯度下降与weight decay的解耦

Adam有很多的优点,但是在很多数据集上的最好效果还是用SGD with Momentum细调出来的。可见Adam的泛化性并不如SGD with Momentum
原因:大部分的模型都会有L2 regularization约束项,因此很有可能出现Adam的最终效果没有sgd的好
量子学园:一文看懂各种神经网络优化算法:从梯度下降到Adam方法
优化方法总结以及Adam存在的问题(SGD, Momentum, AdaDelta, Adam, AdamW,LazyAdam)



