数值优化｜笔记整理（8）——带约束优化：引入，梯度投影法

欢迎浏览我公司网站！！

公司动态

时间: 2024-06-24浏览次数：

上一节笔记：学弱猹：数值优化（7）——限制空间的优化算法：LBFGS，LSR1————————————————————————————————————大家好！这一节我们会开辟一个全新的领域，我们会开始介绍带约束优化的相关内容。带约束优化在某些细节上会与之前的内容有所不同，但是主要的思路啥的都会和我们之前的传统方法一致，所以倒也不必担心。那么我们开始吧。带约束优化问题的基本框架

上一节笔记：

学弱猹：数值优化（7）——限制空间的优化算法：LBFGS，LSR1

————————————————————————————————————

大家好！这一节我们会开辟一个全新的领域，我们会开始介绍带约束优化的相关内容。带约束优化在某些细节上会与之前的内容有所不同，但是主要的思路啥的都会和我们之前的传统方法一致，所以倒也不必担心。

那么我们开始吧。

带约束优化问题的基本框架与支撑性质

优化边界举例

梯度投影法
标准化的梯度投影法

D. P. Bertsekas. Nonlinear Programming
C. T. Kelley. Iterative Method for Optimization
课堂笔记，教授主页：

https://www.math.fsu.edu/~whuang2/index.html

一般来说我们会研究的问题长这个样子

$\\min_{x \\in \\mathbb{R}^n}f(x) \\\\ s.t. \\quad x \\in \\mathcal{K}\\subset{\\mathbb{R}^n}$

其中 $f$ 是实值函数，并且在很多情况下，这里的 $\\mathcal{K}$ 都是凸集。在带了约束的情况下，我们的所有的优化步骤都必须局限在约束内。所以自然需要引入很多额外的定义，也就是说在介绍具体的方法之前，我们会用大量的定义和定理为大家构建一个带约束优化问题的框架，这样的话在遇到一些带约束优化特有的情形的时候，就不会感到奇怪。

首先是下面这个定义

Definition 1: Projection
设 $\\mathcal{K}\\subset{\\mathbb{R}^n}$ 为一个在希尔伯特空间内的凸集，那么对任意的 $z \\in \\mathbb{R}^n$ ，我们定义它到 $\\mathcal{K}$ 的投影为 $z^*=\\mathcal{P}z=\\arg\\min_{x \\in \\mathcal{K}}\\|x - z \\|$ ，这里的范数定义为内积生成的范数，也就是 $\\|z\\|^2=\\left< z, z\\right>$ 。

说它是投影也无可厚非，只不过这个投影和单纯的“投影到地面上”啥的相比，做了一个拓展。所以关于这个投影，是否还具有一般的性质呢？这就是下面要说的。

Proposition 1:
设 $\\mathcal{K}\\subset \\mathbb{R}^n$ 是一个凸而闭的集合，那么
(1) 投影存在且唯一。
(2) 对任意的 $z \\in \\mathbb{R}^n$ ， $\\mathcal{P}z=z^* \\in \\mathcal{K}$ 当且仅当 $\\forall x \\in \\mathcal{K}$ ，有 $(z - z^*)^T (x - z^*) \\le 0$ 。
(3) 投影算子 $\\mathcal{P}: \\mathbb{R}^n \ o \\mathcal{K}: z \ o \\mathcal{P}z$ 连续，并且有 $\\forall z, y \\in \\mathbb{R}^n$ ，有 $\\|\\mathcal{P}z - \\mathcal{P}y\\| \\le \\| z - y\\|$ 。

我们证明一下这个结论。第一个看起来好像很难，我们先看第二个。假如说我们有 $(z - z^*)^T (x - z^*) \\le 0$ ，那么注意到投影到的点满足的条件是与原始点的距离最小，所以一个常见的思路就是计算距离，并通过加减项的方式“拆出”我们想要的东西。具体来说，就是对于任意的 $x \\in \\mathcal{K}$ ，有

$\\| z - x\\|^2=\\|z - z^* - (x - z^*)\\|^2=\\|z - z^*\\|^2 + \\|x - z^*\\|^2 - 2 \\left< z - z^*, x - z^*\\right>$

然后只需要带入我们的结论即可（因为欧氏空间中， $\\left< x, y\\right>=x^T y$ ）。

另一方面，假如说我们有 $\\mathcal{P}z=z^* \\in \\mathcal{K}$ ，那么这个时候对于任意的 $x \\in \\mathcal{K}$ ，都会有 $\\|z - z^*\\|^2 \\le \\|x - z^*\\|^2$ 。现在我们假设我们有 $(z - z^*)^T (x - z^*) > 0$ ，那么我们的思路就是沿着 $x - z^*$ 的方向稍微走那么一点，来看看是否有反例。具体为什么这么做我们后面给大家解释。

设 $x_\\alpha=z^* + \\alpha (x - z^*)$ ，那么这个时候，我们有 $z - x_\\alpha=z - z^* - \\alpha(x - z^*)$ ，设 $v_1=z - z^*$ ， $v_2=x - z^*$ ，那么我们有 $z - x_\\alpha=v_1 - \\alpha v_2$ 。那么这个时候不难得到

$\\|v_1 - \\alpha v_2 \\|^2=\\|v_1\\|^2 + \\alpha^2 \\|v_2\\|^2 - 2 \\alpha \\left< v_1, v_2\\right>$

这里要注意的是，根据条件我们有 $\\left< v_1, v_2\\right> > 0$ ，换句话说，一定会存在一个数 $\\alpha$ ，使得 $\\|v_1 - \\alpha v_2\\|^2 < \\|v_1 \\|^2$ ，这就矛盾了，因为一方面我们移动的距离很短，所以可以保证我们的点还在这个集合内，而另一方面，我们有要求过距离最小，但是我现在找到了一个新的点 $x_\\alpha$ ，它的距离可以做到更小，这是不可能的。到此我们就算证明了这个结论。

这一张图说明了这个性质想告诉我们什么，也点出了证明思路。

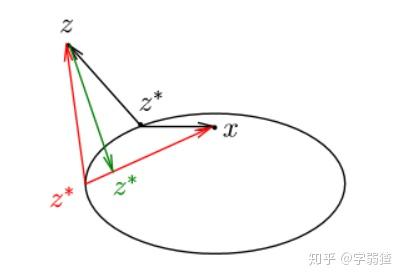
具体说就是，实际情况下，投影到两个我们关心的目标点 $z, x$ 的夹角应该是直角/钝角，如果是锐角的话，那么我们在 $x -z^*$ 这一条线上一定可以找到一个点，使得 $z -z ^*$ 的距离变小，就不再符合投影的定义了。这也就是一个非常简单的“垂线段最短”的道理。

再来说说第三个结论，第三个结论其实就是利用一下我们的不等式。设 $\\mathcal{P}z=z^*, \\mathcal{P}y=y^*$ ，那么我们会有

$\\begin{cases}\\left< z - z^*, y^* - z^*\\right> \\le 0 \\\\ \\left< y -y^*, z^* - y^*\\right> \\le 0\\end{cases}$

简单的组合一下就会有$\\left \\le 0$，这样的话其实不难得到的是

$\\|y^* - z^*\\|^2 \\le \\left< y^* - z^*, y - z\\right> \\le \\|y^* - z^* \\|\\|y -z \\|$

两边约分即可得到我们想要的结果，而这个结果其实就隐含了算子的连续性。

关于第一个性质的证明，其实严格来说算是拓扑学的内容，简单来说，在一个有限闭集上取定义域的连续实值函数是可以取到极大极小值的。具体的细节我们这里不详谈，但是为了方便理解，我们放一个链接

学弱猹：拓扑学Ⅱ|笔记整理（4）——紧致性，列紧性

在这里的Proposition 1有简单点一个类似的性质，虽然不完全一样，但理解够了。

有了这个性质我们说明下面的一个等价性质也就不困难了。

Proposition 2:
设 $\\mathcal{K}$ 为 $\\mathbb{R}^n$ 的子空间（也就是说它是一个凸集），那么 $\\forall z \\in \\mathbb{R}^n$ ， $z^*=\\mathcal{P}z$ 当且仅当 $(z - z^*) \\perp \\mathcal{K}$ 。

简单说明一下，根据 $\\left< z -z^*, x - z^*\\right> \\le 0$ ，分别代 $x=z^* + v, x=z^* - v$ 并保证这两个新的点依然落在这个凸集内，就可以得到 $(z- z^*)^T v=0$ ，这也就说明了结论成立。

这里多说一句，就是虽然我们说 $x \\perp \\mathcal{K}$ 的含义是要求对任意的 $v \\in \\mathcal{K}$ 都要有 $x \\perp v$ ，但是我们这里的写法其实就足够说明这一点了，因为我们取的 $v$ 的方向是任意的，只有它的长度会有要求不能太大，因为要保证 $z^* + v \\in \\mathcal{K}$ 和 $z^* - v \\in \\mathcal{K}$ 。而要说明向量与空间的垂直性，长度这个因素是不用考虑的。

下面我们给出带约束优化问题中，驻点的定义。

Definition 2: Stationary Point
若 $\\forall x \\in \\mathcal{K}$ ，都有 $\ abla f(x^*)^T (x -x ^*) \\ge 0$ ，那么称 $x^* \\in \\mathcal{K}$ 是一个 $f$ 的驻点。

这个定义实质上说明了带约束优化问题中我们对于极小值性质的考虑，而且可以看出来，在区域的内部的时候，可以推出 $\ abla f(x^*)=0$ ，简单来说，你只需要让 $x - x^*$ 的方向取的任意即可。下面这张图给了一个更直观的解释。

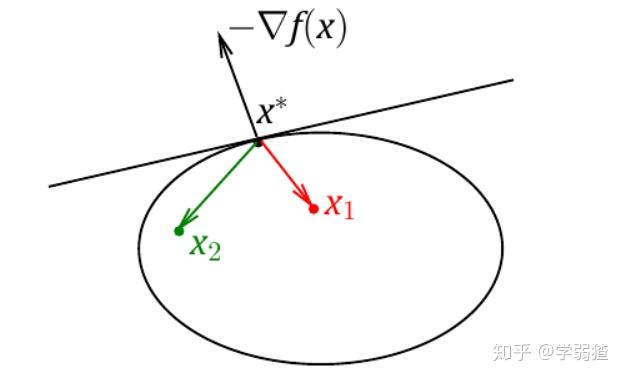
我们说过，只有目前你可以走的方向（这里的 $x^* - x_1$ 与 $x^* - x_2$ ）与负梯度方向成一个锐角才有可能使得值下降，但是在边界上的时候，根据不等式条件你做不到这一点，那么这个时候就无法下降了，那么认为它是驻点自然也是合理的。

接下来我们给出驻点与投影之间的联系。

Proposition 3:
设 $f$ 在 $\\mathcal{K}$ 上是一个连续可微的函数，那么 $x^* \\in \\mathcal{K}$ 为驻点当且仅当 $\\forall \\alpha \\ge 0, x^*=\\mathcal{P}(x^* - \\alpha \ abla f(x^*))$ 。

我们证明一下这个结论。一方面，如果 $x^*$ 为驻点，那么会有 $(-\\alpha \ abla f(x^*))^T (x - x^*) \\le 0$ （因为 $\\alpha \\ge 0$ ）。之后事实上做一个简单的变换就可以得到 $[x^* - \\alpha \ abla f(x^*) - x^*](x - x^*) \\le 0$ ，根据我们的Proposition 1的(2)即可得到结论。

另一方面，如果说我们有 $\\forall \\alpha \\ge 0, x^*=\\mathcal{P}(x^* - \\alpha \ abla f(x^*))$ ，那么这就说明了式子 $[(x^* - \\alpha \ abla f(x^*) )- x^*](x - x^*) \\le 0$ 成立，也就是说我们有 $\ abla f(x^*)^T (x -x ^*) \\ge 0$ ，这就足够说明 $x^*$ 为驻点了。

所以其实对于这个结论，正反只是把话重复了一遍而已，没什么特别的。给出这一个性质作为铺垫，是因为我们后面的算法需要用到。

接下来我们给出局部极小值和驻点之间的关系。

Proposition 4:
设 $x^*$ 为 $f$ 在 $\\mathcal{K}$ 上的极小值，那么 $x^*$ 为驻点。

证明的思路和之前无约束优化的情形是非常类似的，设 $x^*$ 不是驻点，但却是局部极小值，那么我们考虑稍微移动一点 $x^*$ 观察函数值是否会存在下降。根据Taylor展开会有

$f(x^* + \\epsilon (x - x^*))=f(x^*) + \\epsilon (x- x^*)^T \ abla f(x^* + \\sigma \\epsilon(x- x^*))$
由于 $x^*$ 不是驻点，所以我们有 $(x - x^*) ^T\ abla f(x^*) < 0$ ，这就相当于说我们有
$(x- x^*)^T \ abla f(x^* + \\sigma \\epsilon(x- x^*)) < 0$

这是因为，我们的 $\\epsilon$ 是可以取的任意的小的，结合梯度的连续性，我们可以保证这个不等号依然是成立的。有了这个之后，我们就可以得到 $f(x^* + \\epsilon(x - x^*)) < f(x^*)$ ，这就矛盾了。

接下来我们给出全局极小值与驻点之间的关系。

Proposition 5:
设 $f$ 是 $\\mathcal{K}$ 上的凸函数，那么 $x^*$ 为 $f$ 在 $\\mathcal{K}$ 上的全局极小值的充分必要条件是 $x^*$ 为驻点。

我们证明一下这个结论。一方面如果是全局极小值，那么肯定是局部极小值，那么推出驻点就用之前的写法就好。另一方面，如果说 $x^*$ 是驻点，我们的思考就是利用凸函数的性质来帮助我们思考。

事实上，根据凸函数的性质我们可以得到

$f(\\alpha x + (1-\\alpha)y) \\le \\alpha f(x) + (1 - \\alpha)f(y)$

通过简单的变换可以得到

$\\frac{f(y + \\alpha (x - y)) - f(y)}{\\alpha}\\le f(x) - f(y)$

令 $\\alpha \ o 0$ ，根据我们的方向导数的公式（见第一节），我们有 $f(x) \\ge f(y) + (x - y)^T \ abla f(y)$ ，令 $y=x^*$ ，那么结合驻点的性质 $(x - x^*)^T \ abla f(x^*) \\ge 0$ 我们就可以得到 $f(x) \\ge f(x^*), \\forall x \\in \\mathcal{K}$ ，这就足够说明结论了。

当然了，在带约束优化中我们也会碰到一阶信息失效的情况（也就是鞍点）。这个时候我们就需要利用到二阶信息，也就是下面这个性质。

Proposition 6:
若 $x^*$ 为 $f$ 在 $\\mathcal{K}$ 上的局部极小值，且 $f$ 为二阶连续可微的，且 $\\forall x, (x- x^*)^T \ abla f(x^*)=0$ 。那么我们有 $\\forall x, (x -x^*)^T \ abla ^2 f(x^*)(x - x^*) \\ge 0$ 。

这个性质的证明只依赖一步Taylor展开。还是一样，我们只需要利用局部极小值的性质，利用极小值点往任何一个方向走一点点，对应的函数值都比当前的值来的大这样的性质就好，也就是说

$f(x^* + \\epsilon (x -x ^*))=f(x^* ) + \\epsilon (x -x ^*)^T \ abla f(x^*) + \\frac12 \\epsilon^2 (x- x^*)^T \ abla f(x^*) (x - x^*)$

然后结合条件，结合 $f(x^* + \\epsilon(x -x^*)) \\ge f(x^*)$ 就可以得到我们的结论。

推了这么多性质容易审美疲劳，我们来看两个例子，一个是正象限集(Positive Orthant)，也就是 $\\mathcal{O}_+=\\{x \\in \\mathbb{R}^n | x \\ge 0 \\}$ ，相当于要求变量的每一维都是非负。一个是边界集 (Bound Constraints)，也就是 $\\mathcal{B}=\\{x \\in \\mathbb{R}^n | \\alpha_i \\le x_i \\le \\beta_i \\}$ ，其中 $x_i=e_i^T x$ ，也即是 $x$ 的第 $i$ 个元素。

首先我们来看 $\\mathcal{O}_+$ 的情况，我们希望观察的是驻点的一个等价形式。就像我们一直说驻点是优化的关键一样。

一方面，我们设 $x=x^* + e_i$ ，那么这个时候可以推出来

$(x- x^*)^T \ abla f(x^*)=e_i^T \ abla f(x^*)=\\frac{\\partial f}{\\partial x_i}(x^*) \\ge 0$

也就是说驻点需要满足的条件就是偏导非负。

另一方面，设对于某一个 $i$ ， $x_i^* > 0$ ，并且有 $x_i=0.5x_i^*$ ，而对于其它的 $j \ e i$ ，有 $x_j=x_j^*$ ，那么我们会有 $(x- x^*) ^T \ abla f(x^*) \\ge 0$ ，也就是说对于每一个分量，我们都会有 $\\frac{\\partial f}{\\partial x_i}(x^*)(x_i - x_i^*) \\ge 0$ ，这就可以写出一个结果是 $-0.5x_i^* \\frac{\\partial f}{\\partial x_i}(x^*) \\ge 0$ ，那么因为 $x_i^* > 0$ ，结合偏导数非负，就可以得到 $\\frac{\\partial f}{\\partial x_i}(x^*)=0$ ，换句话说，我们的第二个条件就是说，如果当前的维度变量是严格正的，那么就要求当前维度的偏导为0。

总结一下，就是

Proposition 7:
设 $f$ 在 $\\mathcal{O}_+$ 上凸，且 $x^* \\in \\mathcal{O}_+$ 为 $f$ 上的全局极小值，那么当 $x_i^* > 0$ ，有 $\\frac{\\partial f}{\\partial x_i}(x^*)=0$ ，当 $x_i^*=0$ ，有 $\\frac{\\partial f}{\\partial x_i}(x^*) \\ge 0$ 。

所以带约束优化的情况和无约束情况，至少在这个约束条件下，还是略有不同的。

接下来我们来看看 $\\mathcal{B}$ 的情况。事实上证明是类似的，和我们上面一样的写法可以得到

Proposition 8:
设 $x^* \\in \\mathcal{B}$ 为驻点，那么如果 $x_i \\in (\\alpha_i, \\beta_i)$ ，则偏导为0，若 $x_i=\\alpha_i$ ，则偏导非负，若 $x_i=\\beta_i$ ，则偏导非正。

这两个限制条件的讨论，其实某种程度上告诉我们说，在边界上和内部对应的性态会不一样。基于这个原因，我们额外给出了下面的定义，它也会伴随着我们对于带约束优化问题的讨论。

Definition 3: Active/Inactive Sets
定义 $\\mathcal{A}(x)=\\{i | x_i=\\alpha_i / x_i=\\beta_i\\}$ 为 $x$ 这个点对应的激活指标集，定义 $\\mathcal{I}(x)=\\{i | i \ ot \\in \\mathcal{A}(x)\\}$ 为非激活指标集。

这里的激活的含义就是我们的边界是否起到了作用。我们可以看到讨论激活与非激活，是根据指标集来的，所以也对应的会有一些其它的定义产生。

Definition 4: Projection of Set
定义 $\\mathcal{P}_\\mathcal{S}x=\\begin{cases}x_i & i \\in \\mathcal{S}\\\\ 0 & i \ ot \\in \\mathcal{S}\\end{cases}$ 为指标集的投影。

直观来看，就是如果我们只保留了我们所需要的维度的信息，其它的都设置为0。

对于 $\\mathcal{B}$ ，我们要研究极小值的情况就会有些不同。这里的原因自然是在于边界的，不过我们只需要稍微修改一下我们的海塞矩阵即可，具体来说就是

Definition 5: Reduced Hessian
定义限制海塞矩阵 $\ abla^2_Rf(x)$ 满足 $e_i^T \ abla^2_Rf(x)e_j=\\begin{cases}\\delta_{ij}& i \\in \\mathcal{A}(x)/ j \\in \\mathcal{A}(x) \\\\ e_i^T \ abla^2f(x) e_j & others\\end{cases}$ 。

有了这个就比较好介绍下面的性质了

Proposition 9:
设 $x^*$ 为 $f$ 在 $\\mathcal{B}$ 边界下的局部极小值，若 $f$ 在 $x^*$ 的邻域内二次Lipschitz连续可微，那么 $\ abla^2_Rf(x^*)$ 半正定。

我们简单证明一下这个结论。事实上，有了投影的定义之后，就可以把每一个自变量写成下面这个形式

$x^*=\\mathcal P_{\\mathcal A}x^* + \\mathcal P_{\\mathcal I}x^*$

所以按照证明半正定的思路，我们事实上就是要说明 ${x^*}^T \ abla_R^2f(x^*) x^* \\ge 0$ ，按照上面的拆解，事实上只会有两个部分留下来，即 ${\\mathcal P_{\\mathcal A}x^*}^T \ abla_R^2f(x^*) \\mathcal P_{\\mathcal A}x^*$ 和 ${\\mathcal P_{\\mathcal I}x^*}^T \ abla_R^2f(x^*) \\mathcal P_{\\mathcal I}x^*$ （想想为什么？），而剩下的两个部分，一个根据无约束优化的情况可以知道它非负，另外一个通过我们对于限制海塞矩阵的定义可以得到为非负（因为对应的子矩阵是单位阵）。所以和非负，那么自然就说明它半正定了。

关于边界和非边界的最优性条件，我们还有一些额外的定义。

Definition 6: Non-degeneraity / Strict Complementarity
设 $x^* \\in \\mathcal{B}$ ，若 $\\forall x \\in \\mathcal{B}, (x- x^*) ^T \ abla f(x^*) \\ge 0$ ，并且 $\\forall i \\in \\mathcal{A}(x^*)$ ，有 $\\frac{\\partial f}{\\partial x_i}(x^*) \ e 0$ ，那么称其为非退化的驻点。也被称为互补松弛性，因为我们有 $e_i^T \ abla f(x^*) \\begin{cases}=0 & i \\in \\mathcal{I}(x^*) \\\\ \ e 0 & i \\in \\mathcal{A}(x^*)\\end{cases}$ 。

为什么这个性质比较重要呢？从反面思考一下，如果一个点它对应在受约束的地方也没有一个比较好的下降，那么约束存在的意义是什么？事实上下面的性质可以帮助我们说明，如果我们具有非退化性（互补松弛性），那么我们会有一些与极值有关的额外条件。

Proposition 10:
设 $x^* \\in \\mathcal{B}$ 为非退化的驻点， $\\mathcal{A}(x^*)$ 非空，那么存在 $\\sigma > 0$ 使得 $\\forall x \\in \\mathcal{B}$ ，都有 $\ abla f^T(x^*)(x - x^*)=\ abla f^T (x^*) \\mathcal{P}_\\mathcal{A}(x - x^*) \\ge \\sigma \\|\\mathcal{P}_\\mathcal{A}(x - x^*)\\|$ 。

简单说明一下这个结论。第一个等式自然不必多说，因为对于非激活的指标，我们有 $e_i^T \ abla f(x^*)=0$ 。而对于激活的点，事实上我们因为具有非激活的性质，它们的边界上的值非零，换句话说，我们可以找到一个 $\\sigma$ ，使得

$\\begin{cases}e_i^T \ abla f(x^*) \\ge \\sigma & x_i^*=\\alpha_i \\\\ e_i^T \ abla f(x^*) \\le -\\sigma & x_i^*=\\beta_i \\end{cases}$

总结来说就是 $e_i^T \ abla f(x^*) (x_i - x_i^*) \\ge \\sigma |x_i - x_i^*|, \\forall i \\in \\mathcal{A}(x^*)$ 。因此我们自然可以得到

$\ abla f^T (x^*) \\mathcal{P}_\\mathcal{A}(x - x^*) \\ge \\sigma \\|\\mathcal{P}_\\mathcal{A}(x - x^*) \\|_1 \\ge \\sigma \\|\\mathcal{P}_\\mathcal{A}(x - x^*)\\|$

这是因为上面的没有下标的范数指的是2-范数，而 $\\|v \\|_1 \\ge \\|v\\|_2$ 。这是数值分析的内容，感兴趣的同学可以自己去证明一下。

这个性质其实就是为下面的这个定理服务的。

Proposition 11:
设 $\\mathcal{B}\\subset \\mathbb{R}^n$ 为凸集， $f$ 在非退化的驻点的邻域内二次可微。如果 $\ abla^2_Rf(x^*)$ 正定，那么 $x^*$ 就是 $f$ 在 $\\mathcal{B}$ 内的一个局部极小值。

尽管基本的思路还是一样，设 $\\phi(\ au)=f(x^* + \ au(x- x^*))$ ，然后说明无论 $x$ 会怎么取，稍微移动一点之后都会使得函数值不下降，也就是观察 $\\phi(\ au)$ 的函数性质。但这里的证明和无约束优化的情况略有差别，原因就是在于在边界上，极小值的梯度不一定再是0。

为了解决这个问题，我们先求解 $\\phi'(0)$ ，因为这就是 $x^*$ 的一个基本情况。注意到

$\\phi'(0)=\ abla f^T(x^*)(x- x^*)=\ abla f^T(x^*)(\\mathcal{P}_\\mathcal{A}(x - x^*) + \\mathcal{P}_\\mathcal{I}(x - x^*))=\ abla f^T(x^*)(\\mathcal{P}_\\mathcal{A}(x - x^*))$

所以这就化归为两种情况，第一种就是 $\\mathcal{P}_\\mathcal{A}(x- x^*) \ e 0$ ，那么这种情况直接考虑利用上面的性质，可以得到 $\\phi'(0) \\ge \\sigma \\|\\mathcal{P}_\\mathcal{A}(x -x^*)\\| > 0$ ，换句话说无论往什么方向走，函数值都会上升，所以结论是成立的。

第二种就是 $\\mathcal{P}_\\mathcal{A}(x- x^*)=0$ ，那么这个时候可以得到 $\\phi'(0)=0$ ，并且

$\\phi''(0)=(\\mathcal{P}_\\mathcal{I}(x - x^*))^T \ abla ^2 f(x^*) (\\mathcal{P}_\\mathcal{I}(x - x^*))$

这个地方注意到，相当于对于非激活的部分保留了原始的数据，而事实上，对于激活的部分，我们给它的海塞矩阵添加什么内容都没关系，因为它们的对应的维度都是0。所以事实上我们可以得到

$\\phi''(0)=(x- x^*)^T\ abla^2_Rf(x^*)(x- x^*) > 0$

这是因为既然添加什么都可以，那不如就添加一个单位矩阵了。而横正也是因为限制海塞矩阵的正定性。换句话说，在原点它的梯度为0，但是二阶导数恒正。这就是无约束优化的情况下极小值的等价性质，因此结论就成立了。

梯度投影法的基本思路和之前的最速下降法非常类似，也是一个相对来说很古老的用于解决带约束优化问题的方法。在此之前我们先介绍几个与投影有关的性质。

Proposition 12:
设 $x \\in \\mathcal{K}$ ， $z=x - \\alpha \ abla f(x), \\alpha > 0$ ，设 $x(\\alpha)=\\mathcal P z$ ，那么有 $\\forall y \\in \\mathcal K, (y - x(\\alpha))^T (x - x(\\alpha)) \\le \\alpha (y - x(\\alpha))^T \ abla f(x)$ , $\\|x - x(\\alpha)\\|^2 \\le \\alpha ( x - x(\\alpha))^T \ abla f(x)$ 。

事实上，这里的两个不等式，如果第一个证明出来了，第二个直接设 $y=x$ 就可以得到了。这里注意到，根据我们的条件和Proposition 1，可以得到

$\\forall y \\in \\mathcal K, z \\in \\mathbb R^n, (y - \\mathcal Pz)^T (z - \\mathcal P z) \\le 0$

然后带入 $z=x - \\alpha \ abla f(x)$ 即可。

这些证明出来的不等式的一个最直接的推论就是

$\\alpha (x (\\alpha ) - x)^T (- \ abla f(x)) \\ge \\|x - x(\\alpha)\\|^2$

这句话的意思就是，我们选择的方向与负梯度方向呈锐角。注意我们的这个性质中，我们的前进方向受到投影的影响，不一定是严格的负梯度方向。但是有了一个锐角的结论，其实也算够用了。

接下来，我们祭出两个最常见的梯度投影法的形式，并给出它们对应的Armijo步长选取条件。

这两种形式分别对应为可行方向（feasible direction）形式和弧（arc）形式，它们俩对应的Armijo条件也略有不同。

Definition 7: Feasible Direction Armijo Condition
设 $\\bar x=\\mathcal P (x - \\sigma \ abla f(x)) \\in \\mathcal K$ ，且 $\\sigma > 0$ ，设 $0 < \\gamma < 1, 0 < \\beta < 1$ ，那么如果 $\\alpha=\\beta^m \\bar \\alpha$ 为使得 $m$ 取值为最小的满足 $f(x + \\alpha ( \\bar x - x)) - f(x) \\le \\alpha \\gamma \ abla f^T(x)(\\bar x - x)$ 的 $\\alpha$ ，则称其满足可行方向情况下的Armijo条件。

这句话直接理解不是特别容易，直观来说和最开始介绍的线搜索方法的步长选取条件相同，也就是说我们的选取策略就是刚开始先找一个基准 $\\bar \\alpha$ ，然后每一步都缩小一个常数 $\\beta$ ，当满足那个不等式之后就停止迭代了。

对于arc形式的，要求也是差不多的

Definition 8: Arc Armijo Condition
设 $\\bar \\alpha > 0, 0 < \\beta < 1, 0 < \\gamma < 1$ ，那么如果 $m$ 是最小的使得 $\\alpha=\\beta^m \\bar \\alpha$ 且使得 $f(x(\\alpha)) - f(x) \\le - \\frac \\gamma \\alpha \\|x - x(\\alpha)\\|^2$ 成立，那么称 $\\alpha$ 满足弧情况下的Armijo条件。

哦，这两个翻译实在是太烫嘴了……

提到步长选取条件必然离不开步长的存在性。对于feasible direction form，这个不困难，因为我们是先投影，再下降的，所以下降方向的性质比较明确。但是对于arc form情况不太一样，因为arc form是先下降，再投影，那么你最后一步究竟把点投到哪里去了，就不好直观的看出来。因此我们需要一些其它的工具。

Proposition 13:
设 $f: \\mathbb R^n \ o \\mathbb R$ 为一个 $C^1$ 的函数， $\ abla f(x)$ 为Lipschitz连续的，且常数为 $L$ 。如果 $x=y+ z$ ，那么我们有
$f(x) - f(z)=y^T \ abla f(x) + \\int_0^1 (\ abla f(x - \ au y) - \ abla f(x))^T y d\ au$ $\\|\\int_0^1 (\ abla f(x - \ au y) - \ abla f(x))^T y d\ au \\| \\le \\frac{L \\|y\\|^2}{2}$

我们证明一下这个结论。事实上，我们可以看出 $z=x - y$ ，所以通过Taylor展开就可以得到

$f(z)=f(x) - \\int_0^1 \ abla f(x - \ au y)^T y d\ au=f(x) + \ abla f(x)^T(z - x) - \\int_0^1 (\ abla f(x - \ au y) - \ abla f(x))^T y d\ au$

这就证明了第一个式子。第二个式子也不难得到为

$\\|\\int_0^1 (\ abla f(x - \ au y) - \ abla f(x))^T y d\ au \\| \\le \\int_0^1 \\|\ abla f(x - \ au y) - \ abla f(x)\\|d\ au \\|y\\| \\le \\int_0^1 L \ au d\ au \\|y\\|^2=\\frac{L \\|y\\|^2}{2}$

这就证明了第二个式子。

有了这个性质之后，我们就会有下面这个结论成立。

Proposition 14:
设 $\ abla f(x)$ Lipschitz连续，且Lipschitz常数为 $L$ ，那么对于 $0 < \\alpha \\le \\frac{2 ( 1 - \\gamma)}{L}$ ，Armijo条件都可以成立，换句话说，步长收缩存在一个下界 $\\alpha_-=\\frac{2\\beta (1 - \\gamma)}{L}\\le \\beta^m \\bar \\alpha=\\alpha$ 。

要证明它，自然需要依赖上面的这个性质。注意到我们关注的是arc form，所以事实上有

$f(x) - f(x(\\alpha))=\ abla f(x)^T (x - x(\\alpha)) + \\int_0^1 (\ abla f(x - \ au x(\\alpha)) - \ abla f(x))^T x(\\alpha) d\ au$

我们的目的是要说明条件成立，所以一定要构造出一个相关的不等式来。事实上我们可以分开来看，注意到

$\\alpha \ abla f(x)^T(x -x(\\alpha)) \\ge \\|x - x(\\alpha)\\|^2$ $\\int_0^1 (\ abla f(x - \ au x(\\alpha)) - \ abla f(x))^T x(\\alpha) d\ au \\ge \\frac L 2 \\|x - x(\\alpha) \\|^2$

所以通过一层绝对值不等式，我们可以得到

$f(x) - f(x(\\alpha)) \\ge \\frac 1 \\alpha ( 1 - \\frac{\\alpha L}{2}) \\|x - x(\\alpha)\\|^2$

仔细观察这个式子与Armijo条件的差异，事实上只是差距在系数 $1 - \\frac{\\alpha L}{2}$ 上。换句话说，我们只需要让 $\\gamma \\le 1 - \\frac{\\alpha L}{2}$ 就可以了，简单化简一下不等式，就可以得到我们的结论。

通过这个结论，也就不难得到我们的最终步长的下界就是 $\\frac{2\\beta (1 - \\gamma)}{L}$ 。换句话说，我们的步长不断的缩小的情况下，不会产生一直找不到步长的情况，这也就是步长的存在性了。

当然了，相信大家也会很关注它们的收敛性。我们列在这里但不会证明。

Theorem 1:
设 $f$ 连续可微， $\ abla f(x)$ Lipschitz连续，且Lipschitz常数为 $L$ ， $\\mathcal{K}$ 是凸而紧的，那么无论使用feasible direction形式，还是使用arc形式的Armijo条件和对应的梯度投影法，都会收敛到驻点。

标准化的梯度投影法（Scaled Gradient Projection Method）是一种针对不同的投影量度而做的对应的修改。简单来说，我们一开始的投影的定义为

$\ ilde z=\\mathcal P (z)=\\arg\\min_{ x \\in \\mathcal K}\\| x - z \\|^2$

但是很多时候我们也会定义它为

$\ ilde z=\\mathcal P_B (z)=\\arg\\min_{ x \\in \\mathcal K}\\| x - z \\|_B^2$

其中 $\\|x - z \\|^2_B=(x - z)^T B (x - z)$ ，所以你也能看出来， $\\forall x \\in \\mathcal K$ ，我们都要求 $(x - z)^T B (x - z ) \\ge 0$ 。

它的具体的算法流程如下

这个方法也具有一定的收敛性，具体如下。同样的，我们也会略过证明。

Theorem 2:
设存在 $0 < c_1 \\le c_2$ 使得 $c_1 \\|z \\|^2 \\le z^T B_k z \\le c_2 \\|z \\|^2, \\forall z \\in \\mathbb{R}^n, \\forall k$ ，并设算法使用了feasible direction或arc形式的Armijo条件，那么算法也使得迭代点收敛到驻点。

对于为什么我们要做投影量度的变换，很多时候就是为了投影的计算方便，但是我们不会在这里提更多的细节。

好的，关于梯度投影法我们就说那么多。大家可以看出，对于这个方法我们没有太多的着力，也是因为它实在是有点古老了。但是这个方法的流程也可以一定程度上帮助大家理解带约束优化的执行过程。

本节我们主要是在构建一个理解带约束优化问题的框架，同时我们花很少的篇幅给大家介绍了梯度投影法。当然了，它都不算是带约束优化问题的主流，之后介绍的KKT条件和一些运筹的方法会带领大家更深刻的看待这一类问题。

——————————————————————————————————————

本专栏为我的个人专栏，也是我学习笔记的主要生产地。任何笔记都具有著作权，不可随意转载和剽窃。

个人微信公众号：cha-diary，你可以通过它来获得最新文章更新的通知。

《一个大学生的日常笔记》专栏目录：笔记专栏|目录

《GetDataWet》专栏目录：GetDataWet|目录

想要更多方面的知识分享吗？可以关注专栏：一个大学生的日常笔记。你既可以在那里找到通俗易懂的数学，也可以找到一些杂谈和闲聊。也可以关注专栏：GetDataWet，看看在大数据的世界中，一个人的心路历程。我鼓励和我相似的同志们投稿于此，增加专栏的多元性，让更多相似的求知者受益~

上一篇：苹果 Apple Arcade 十月新增游戏包括《NBA 2K24》等等

下一篇：优化营商环境的心得体会（精选21篇）

粤IP*******